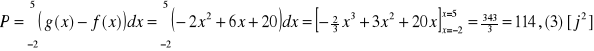Pole pod krzywą a całka oznaczona

Zadanie 1. Obliczyć pole trójkąta krzywoliniowego ograniczonego parabolą o równaniu
w przedziale
i osią odciętych.

Pole obliczymy za pomocą całki oznaczonej:

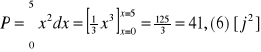
Powyższy rezultat możemy sprawdzić na kalkulatorze CASIO fx-9860:

Zadanie 2. Obliczyć pole obszaru ograniczonego wykresem funkcji
i osią odciętych.

Zacznijmy od rysunku:

A więc pole jest sumą dwóch pól, pola P₁ obszaru położonego powyżej osi odciętych i pola P₂ obszaru położonego poniżej osi odciętych, mamy przy tym

,

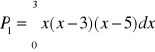
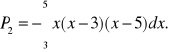
Dalej,

a więc

,

stąd

Sprawdźmy za pomocą kalkulatora CASIO fx-9860:

Zadanie 3. Obliczyć pole obszaru ograniczonego parabolami
i
.

Zacznijmy od rysunku:

Odcięte punktów przecięcia obliczymy rozwiązując równanie
, lub odczytamy z kalkulatora:

A więc