Michał Borawski Inż. Środ. gr.1

Ćwiczenie 42. Wyznaczanie oporu elektrycznego metodą mostka Wheatstone'a

Wstęp:

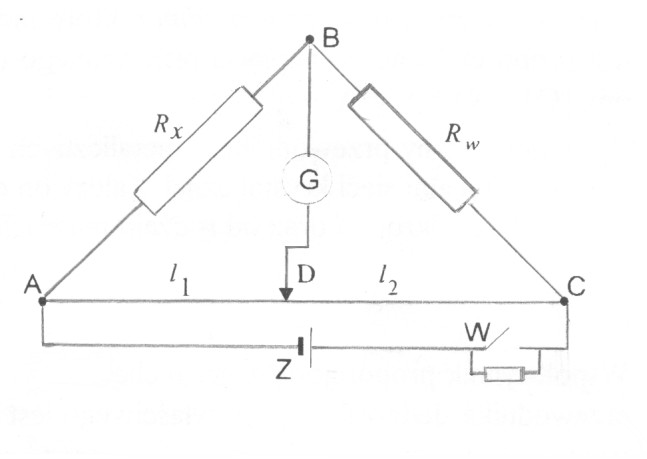
Celem ćwiczenia jest wyznaczenie oporu R_x, który łączymy szeregowo z oporem wzorcowym R_w. Jedną z prostszych i dokładniejszych metod pomiaru oporu jest porównawcza metoda liniowego mostka Wheatstone'a. W celu wykonania ćwiczenia wolne końce połączonych oporników łączymy z punktami A i C, pomiędzy którymi rozpięty jest drut oporowy wzdłuż podziałki milimetrowej. Punkt B, wspólny dla oporów R_x i R_w, łączymy poprzez miliamperomierz G z suwakiem D, który może swobodnie ślizgać się po drucie. Włączając zasilacz Z prądu stałego, przykładamy napięcie do punktów A i C. Następnie szukamy takiego położenia suwaka D na strunie, aby przez odcinek BD prąd nie płynął.

Wykonanie ćwiczenia:

Pierwsza czynność polega na zestawieniu obwodu elektrycznego zgodnie ze schematem widocznym poniżej, przy czym: R_w - opornik wzorcowy dekadowy, R_x - opornik badany, Z - źródło prądu stałego, G - galwanometr (miliamperomierz), W - wyłącznik z oporem zabezpieczającym.

Następnie przy otwartym wyłączniku W ustawiamy opornicę dekadową na wartość 10Ω i włączamy zasilacz Z. Dobieramy położenie suwaka D na strunie tak, aby galwanometr wskazywał wartość zero. Po zamknięciu klucza W położenie to ustalamy bardziej precyzyjnie i odczytujemy długości odcinków l₁ i l₂. Po odczytaniu tych wartości obliczamy wartość szukanego oporu - jest to wartość orientacyjna, obarczona dość dużym błędem pomiarowym. Oznaczamy wyznaczoną wartość R_x jako R₀.

Postępując jak wyżej wykonujemy trzy pomiary oporu R_x: ustawiamy na opornicy dekadowej kolejno trzy różne, ale bliskie R₀ wartości oporu wzorcowego. Otrzymujemy w ten sposób trzy wartości R₁, R₂, R₃. Jako wartość oporu R_a przyjmujemy średnią arytmetyczną równą (R₁+R₂+R₃)/3. Identycznie wyznaczamy opór następnego opornika - R_b.

W następnej części ćwiczenia łączymy badane oporniki szeregowo i dokonujemy pomiaru oporu wypadkowego za pomocą mostka Wheatstone'a. Tak samo postępujemy w przypadku połączenia równoległego.

Rachunek błędów:

Błąd względny pomiaru, ∆R_x/R_x, obliczamy ze wzoru:

Obliczam błąd względny pomiaru
dla przewodnika
wykorzystując w tym celu pomiar nr 0, w którym wartości
i
odbiegają najbardziej od zalecanego ustawienia suwaka tzn. w połowie długości struny.

Następnie obliczam błąd względny dla pomiaru nr 3, w którym wartości
i
są najbliższe zalecanego ustawienia suwaka na strunie.

Na podstawie otrzymanych wyników mogę przypuszczać, że pomiary nr 1 i 2 zawierają się między
,a
.

Skoro wyniki powyższych obliczeń spełniają założenia ćwiczenia - (jeśli wartości
i
są sobie równe -to błąd pomiaru jest najmniejszy). W związku z tym wystarczy obliczyć błąd względny pomiaru nr 0 dla przewodnika
, gdyż odbiega on najbardziej od zalecanego ustawienia suwaka na strunie. Błędy pozostałych pomiarów będą mniejsze niż ta wartość.

Tak, więc błąd pomiarów nr 1,2 i 3 jest mniejszy niż
.

Wnioski:

Wartość oporu badanego zależy bezpośrednio od położenia suwaka na strunie i oporu wzorcowego. Wraz z jego wzrostem rośnie także wartość oporu badanego. Natomiast opór właściwy przewodnika zależny jest od jego przekroju, oporu badanego i długości. Gdy wzrostowi ulega przekrój bądź opór badany, wówczas rośnie opór właściwy. Jeśli rośnie długość przewodnika to opór właściwy maleje. Pole przekroju przewodnika jest wprost proporcjonalne do jego długości i średnicy. Ponieważ średnica konstantanu jest mniejsza od średnicy stali, zatem jego przekrój jest także mniejszy. Nie oznacza to jednak, że jego opór właściwy jest mniejszy od oporu właściwego stali. Znaczenie ma tutaj także wartość oporu badanego, który dla stali jest o wiele mniejszy.

Najprawdopodobniej błąd, (choć nie duży) wynikać może z trudności z bardzo dokładnym odczytem wartości długości
i
, jak również najmniejszej wartości przesunięcia suwaka na strunie, dla której występuje zauważalne przemieszczenie wskazówki galwanometru. Kolejnym powodem może być stan techniczny urządzeń użytych do pomiarów.

---