0050

51
§ 2. Twierdzenia o granicach ułatwiające znajdowanie granic
W celu znalezienia granicy przedstawmy p(n) w postaci:
/ - */ . . . a*-» .
p(n) = n (ooH---K..H—+
\ n n n)
Ponieważ wszystkie wyrazy w nawiasach, poczynając od drugiego, przy n-»oo dążą do zera, więc wyrażenie w nawiasach ma granicę a0; pierwszy czynnik dąży do + oo. Tak więc całe wyrażenie dąży do + oo lub do —oo, w zależności od znaku a0.
Przekształcenie wyrażenia (czym się tu posłużyliśmy) często pomaga w znalezieniu granicy.
2) Jeżeli q(n) jest podobnym wielomianem
q(n)=b0 nl+bln~1 -r.-.+bt-i n+b,,
to iloraz p(n)!q(ri) przy n-*oo przedstawia wyrażenie nieoznaczone postaci oo/oo.
Przekształcając i tu każdy z wielomianów, jak w przykładzie 1), otrzymujemy
, “i ak
a0-r-—h... H—j-P(n)_ t_i n__n
bo H---h. ■ • i—y
Drugi czynnik ma skończoną granicę a0jb0. Jeżeli stopnie obu wielomianów są równe: k = I, to tę samą granicę ma iloraz p(n)lq(n) (‘).
Przy k>l pierwszy czynnik dąży do +oo, czyli rozważane wyrażenie dąży do ±oo (zależnie od znaku a0lb0). Na koniec przy k<l pierwszy ®-ys- 3
czynnik dąży do zera, a wraz z nim całe wyrażenie.
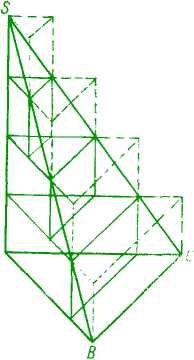
3) Znaleźć objętość V ostrosłupa trójkątnego SABC (rys. 3).
Dzieląc wysokość H ostrosłupa na n równych części, poprowadźmy przez punkty podziału płaszczyzny równoległe do płaszczyzny podstawy. W przekroju otrzymujemy trójkąty podobne do podstawy. Zbudujmy na nich układ wpisanych i opisanych graniastosłupów: z pierwszych tworzymy bryłę o objętości V„, z drugich bryłę o objętości V'„, przy czym oczywiście
K<V<V'n.
Ale różnica PJ— V„ jest po prostu objętością dolnego wystającego graniastosłupa o polu podstawy Q równym polu A ABC i wysokości H/n; tak więc różnica
QU
—>o
n
przy wzroście n, a więc tym bardziej dążą do zera różnice V—Vn i V'„—V, tj.
K=lim P„=lim K'.
Znajdziemy teraz wyrażenie na Mamy tu bryłę, składającą się z szeregu graniastosłupów: z własności przekrojów ostrosłupa wynika, że podstawy tych graniastosłupów są równe:
22
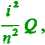
0) Tak można było otrzymać granicę J w przykładzie 4) ustępu 25.
Wyszukiwarka