005 2

4.

Zeemanowskie widmo EPR atomu i cząsteczki

Zajmiemy się teraz niesparowanym elektronem znajdującym się w atomie lub cząsteczce. Zakładamy, że spin jąder atomów jest równy zeru. Pierwszym krokiem teoretycznego opisu jest podanie hamiltonianu spinowego. W hamiltonianie należy uwzględnić oddziaływanie pola magnetycznego ze spinowym momentem magnetycznym fi_s (zgodnie z wyrażeniem (3.1)), oddziaływanie pola magnetycznego z orbitalnym momentem magnetycznym iu_L= "H_bL oraz oddziaływanie (sprzężenie) spinowo-orbitalne L Ś. Hamiltonian ma teraz następującą postać:

H^gtigB-Ś+tigBL + ALŚ.    (4.1)

Największe trudności sprawia człon L Ś, który uniemożliwia dokładne obliczenie wartości i funkcji własnych hamiltonianu. Znajomość wartości własnych energii, jak było pokazane dla elektronu swobodnego, jest niezbędna do wyznaczenia pola rezonansowego.

W celu wyznaczenia przybliżonych wartości energii stosuje się metodę rachunku zaburzeń. Ponieważ hamiltonian (4.1) zawiera operatory spinu i momentu orbitalnego, więc w funkcjach falowych obok części spinowej wyraźnie zaznaczymy znakiem G ich część orbitalną. Poprawki ł oraz 2 rzędu do energii należy obliczyć według wzoru:

+    = <0, Ms\H\G, Ms> + £

„ <G, Ms\H\n> <n\H\G, Ms>

(4.2)

gdzie Ej, oznacza sumowanie po wszystkich stanach z wyjątkiem rozważanego stanu jG, Ms). Wykonanie tych obliczeń jest żmudne, więc ograniczymy się do podania ogólnych informacji o tak obliczonych poprawkach:

1)    poprawki do energii zależą od wartości indukcji pola B,

2)    poprawki mogą zależeć od orientacji cząsteczki w stosunku do pola magnetycznego; jest to związane z typem symetrii centrum paramagnetycznego,

3)    oddziaływanie AŁ Ś powoduje tzw. rozszczepienie w zerowym polu magnetycznym; rozszczepienie to jest obserwowane w widmach ze strukturą subtelną i będzie rozważone w rozdz. 6.

Warunek rezonansu ma teraz postać:

(4.3)

AE(B_m, 3, 4) = hv,

a pole rezonansowe'będzie zależeć od orientacji cząsteczki (kąty 9, w układzie sferycznym) względem pola magnetycznego.

Rachunek zaburzeń pozwala też obliczyć poprawki do funkcji, np. poprawkę 1 rzędu obliczamy według wzoru:

|G»

,<G, Ms|HU)

^Łn (£B*-Ą^0ł)

(4.4)

Z tego wzoru wynika możliwość „mieszania” się stanów o różnym momencie orbitalnym. Stan podstawowy większości molekuł charakteryzuje się zerowym momentem orbitalnym; oddziaływanie czysto spinowe stanu podstawowego ze stanem wzbudzonym, mającym udział momentu orbitalnego, wnosi wkład orbitalny również do stanu podstawowego.

Rozważymy teraz trzy orientacje cząsteczki w stosunku do pola magnetycznego; układ współrzędnych wybieramy zgodnie z symetrią centrum paramagnetycznego. Przy niskiej symetrii centrum paramagnetycznego wykresy przybliżonych wartości energii, obliczone rachunkiem zaburzeń, mogą mieć postać:

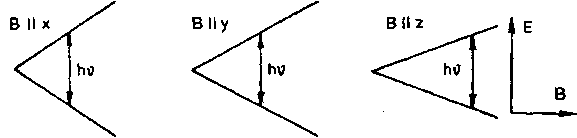
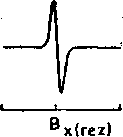
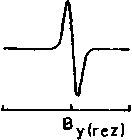
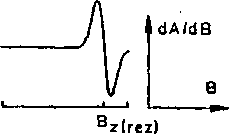
Rys. 4.). Wykresy poziomów energetycznych oraz widm dla trzech orientacji cząsteczki w polu magnetycznym

Podane na rys. 4.1 widma są otrzymane dla odpowiednio zorientowanych monokryształów. Jak widać z rysunku, dla tych orientacji linie absorpcji wystąpią przy różnych polach rezonansowych. Każda pośrednia orientacja dałaby linię pomiędzy minimalnym polem B^zj a polem maksymalnym 2?,_(rez); jest to bardzo ważny fakt, zwłaszcza przy omawianiu widm proszków lub cieczy zamrożonych. ^Zmiany energii poziomów, dla danej orientacji, są podobne jak dla elektronu swobodnego (wzory (3.7)). W zależności od