005

Częstotliwość rezonansowa wynosi
t.±.iL ^r 2tt y CL	-0	(1.4)
lub po przekształceniu
f - U	i-R’ C	(1.5)
’ 2K-JLĆ j	L C
Jeśli R « J— , to fr =-7= • VC 2jiVLC		(16)

Częstotliwość rezonansowa jest liczbą rzeczywistą, jeśli:

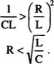
Związek (1.7) między parametrami obwodu warunkuje występowanie rezonansu w obwodzie jak na rys. 1.1.

Przykład 2.

Analizując następny obwód elektryczny przedstawiony na rys. 1.2 wykażemy, że ma on więcej niż jedną częstotliwość rezonansową.

L1

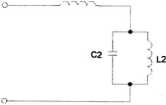
Rys. 1.2

42 ¹ <i>^!L₂C, -1

Z = jcoL| +

jrnLj^	^JfflC2)
/ .	_ • )
	coC2 J

*j <"L| —

Impedancja zespolona zawiera tylko składową urojoną. Aby nastąpił rezonans musi być spełniony następujący warunek:

łm{z}= (OL, -    =

¹ o)²L₂C₂-1

-L₍ -L₂)=0 „² _ L|⁺L₂

ę=E±ŁI

V L|LjC₂

f ₌_L )l,+l₂

¹ 2tt L,L₂C₂

Dla tej częstotliwości zachodzi rezonans napięć na cewce L| i na dwójniku C₂,

	[<oC2	' ] ^1	cd^2L2C2 -1
		g)L2 jjcoL,	toL2
i		^1 1 i	^Ju>Lf<0C ' ' 1
^J|	toc ux^2	coL, <oL2 J	“^L,(^^2 toL, o>L2 J

to²L₂C₂ -1

coL₂ _ .    (0²L₂C₂-1

''a.=L₁C₂^l^''^J^L_lL₂C₂-L_l-L₂)

lm{Y}=0 <i)L,C₂-1 = 0

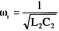
43