008 3
14
ma możliwość wymiany energii z otoczeniem. Może to być wymiana z nie-sparowanym elektronem z sąsiedniej cząsteczki (tzw. relaksacja spin-spin) tub z innym obiektem (relaksacja spin-sieć, przejścia przez stany pośrednie, np. translacyjne, oscylacyjne). Aby nie nastąpiło zjawisko nasycenia, proces relaksacji powinien zachodzić wystarczająco szybko. Czas relaksacji definiuje się jako czas, w którym liczba układów w stanie wyższym zmniejszy się \/e (as 0,36) razy. Czas relaksacji jest zatem miarą czasu życia układu (w sensie statycznym) w danym stanie i wpływa na szerokość linii EPR zgodnie z zasadą Heisenberga
d£dt~fc/2jr, (5.4)
gdzie ńE jest nieokreślonością („rozmyciem”) energii danego poziomu (nie mylić z różnicą energii między poziomami; z nieokreśloności energii poziomu wynika nieokreśloność różnicy energii). Jeśli czas relaksacji spin-sieć oznaczyć przez Tlt a czas relaksacji spin-spin przez T2, to
szerokość linii EPR « l/T, + l/T2. (5.5)
Na wydłużenie czasu relaksacji spin-sieć wpływa się przez obniżenie temperatury próbki. Czas relaksacji spin-spin wydłużamy przez zwiększenie średniej odległości między spinami w sąsiednich cząsteczkach oraz przez eliminację innych poziomów spinowych. Odległości między spinami zwiększamy przez rozcieńczenie próbki diamagnetykiem; obecność innych poziomów spinowych eliminujemy usuwając zanieczyszczenia paramagnetyczne w układzie.
6. Widma EPR ze strukturą subtelną
Struktura subtelna widm EPR pojawia się w przypadku obecności co najmniej dwóch niesparowanych elektronów w cząsteczce. Rozważmy układ z dwoma niesparowanymi elektronami. Spin całkowity układu przyjmuje wartości 0 oraz 1. Stan z S = 0 jest oczywiście nieaktywny w badaniu metodą EPR i wystarczy rozważyć stany z S=1 (tzw. tryplet; St = —1,0, -fi). Efektywny hamiltonian ma postać
J? = /iBB-g-jr+0{S?-l/3S(S+l)} + £(^-S;). (6.1)
Parametry D i £ opisują rozszczepienie trypletu spinowego w zerowym polu magnetycznym i są związane z symetrią układu. Rysunek 6.1 przedstawia przykład rozszczepienia poziomów spinowych oraz widmo monokryształu o osiowej symetrii:
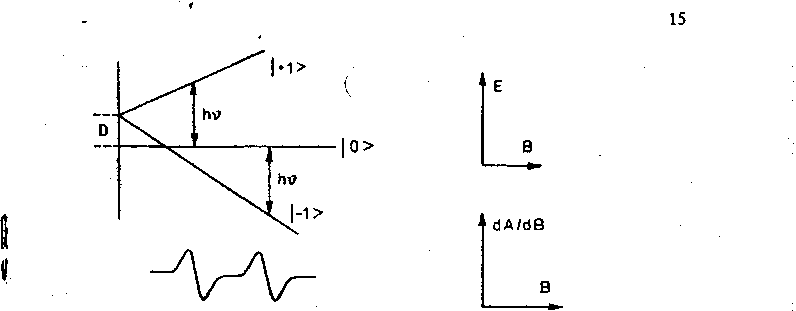
Rys. 6.1. Poziomy energetyczne i widmo subtelne monokryształu. S= 1, £||z, D>0, £ = 0
Gdyby parametr D był równy zeru, zamiast dwóch linii otrzymalibyśmy jedną. Ponieważ zaznaczone stany nie są czystymi stanami rzeczywistego spinu, więc czasem obserwuje się słabą linię dla „wzbronionego" przejścia
l-OH + i).
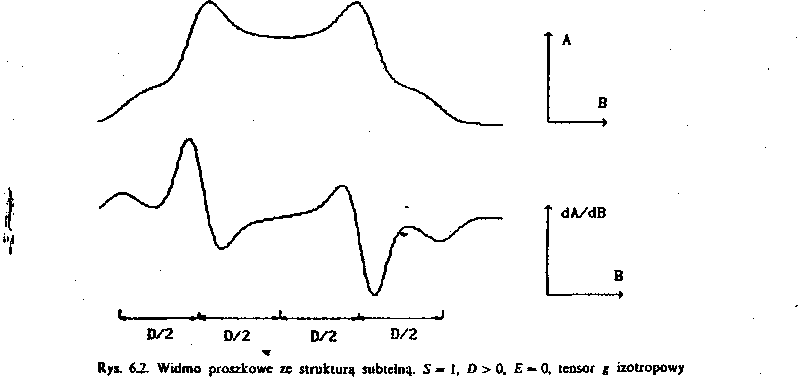
Widma proszkowe ze strukturą subtelną, anizotropią tensora g oraz strukturą nadsubtełną i supernadsubłelną (rozdz. 7) są bardzo skomplikowane. Do ich interpretacji często używa się programów komputerowych (tzw. programy symulacji widm). Poniżej (rys. 6.2) podany jest przykład widma proszkowego (obliczonego programem komputerowym) ze strukturą subtelną:
Wyszukiwarka