00098466

148 RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE

Przykład 3. Znaleźć całkę ogólną równania

Niech A będzie dov funkcję klasy C w

obszarem przestrzeni trójwymiarowej. Jeżeli h(x,y) oznacza dowolną us O, będącym rzutem prostokątnym obszaru A na płaszczyznę Oxy, to «(-r.y. z) - K*.y)    (n.li)

Znaleziona całka ogólna zależy od jednej dowolnej funkcji dwóch zmiennycl).

Uwaga. Na podstawie powyższych przykładów mogłoby się wydawać, ze całka ogólna równania różniczkowego cząstkowego rzędu pierwszego zależy od jednej funkcji dowolnej, całka ogólna równania rzędu drugiego od dwóch dowolnych funkcji itd. Przypuszczenie to w ogólnym przypadku jest jednak błędne.

Zagadnienie Cauchy'ego. W teorii równań różniczkowych cząstkowych poszukuje się najczęściej rozwiązań nie tylko dostatecznie regularnych, lecz spcłniąją-cych ponadto pewne dodatkowe warunki. Te dodatkowe warunki określające rozwiązanie szczególne (nie zawsze w sposób jednoznaczny) nazywamy warunkami granicznymi.

W zależności od interpretacji fizycznej zagadnienia warunki graniczne nazywamy warunkami początkowymi albo warunkami brzegowymi. Obecnie omówimy podstawowe w teorii równań różniczkowych cząstkowych zagadnienie z warunkami początkowymi.

Niech będzie dane równanie różniczkowe cząstkowe rzędu pierwszego

du

óx

01.12)

dy ’ dz )

w którym u = u(x, y, z) jest funkcją niewiadomą,/!(o,, i>₂,..., o₆) zaś jest funkcją daną, określoną w pewnym obszarze £2, c E₆.

Zagadnienie Cauchy'ego dla równania (II.I2) polega na wyznaczeniu takiego rozwiązania u = u{x,y, z) tego równania w obszarze Z), <= E_s, które spełnia warunek początkowy

u(x₀,y,z) = <plj>,z)    (UJ3)

przy czym liczba x₀ oraz funkcja (Ky, z) określona w obszarze D\, który jest rzutem obszaru />, na płaszczyznę Oyz, są z góry dane.

Warunek (11.13) oznacza, że na płaszczyźnie x = x₀ rozwiązanie ii(x,y, z) ma prżyjmować z góry dane wartości.

Niech z kolei będzie dane równanie różniczkowe cząstkowe rzędu drugiego

01.14)

d²u . I    du Óu_ d²u

~dxⁱ    />*< > >    ..... dt ¹ dxdy'

w którym u= u{x,y, z, t) jest funkcją niewiadomą, /»(*>,,v₂,.. . ®ia) zaś jest funkcją daną, określoną w pewnym obszarze Słi <= J?_łB.

Zagadnienie Cauchy'ego dla równania (11.14) polega na wyznaczeniu takiego rozwiązania u u{x,y,z,i) tego równania w obszarze Dj <= £₄. które spełnia warunki początkowe

tĄx_a,y,z,t) -<p(y,z,t), u_x(x_a,y,z, /)»=■ y(y,z< 0 (n.is) przy czym liczba x₀ oraz funkcje <p(y, z, f) i y(y, z, t) określone w obszarze Oj są z góry dane.

U w a s a. Obszar D'₂ będący dziedziną funkcji f(y, i, i) i ę>0>, t, r) jest obszarem przestrzeni E) złożonym ze wszystkich punktów, których współrzędne są trzema ostatnimi współrzędnymi dowolnego punktu obszaru D, c- /T,

Liczbę x₀ oraz funkcję <p(y, z) w przypadku zagadnienia Cauchy’ego dla równania (11.12) lub odpowiednio liczbę x₀ oraz funkcje <f(y, z, t) i y(y,z,t) w przypadku zagadnienia Cauchy’ego dla równania (n.14) nazywamy wartościami początkowymi.

Przykład 1. Znaleźć całkę szczególną równania u,-u,— 0określoną na całej płaszczyźnie Oxy i spełniającą warunek początkowy. «(0, j>) =» y¹.

Zgodnie z (IL9) całka ogólna tego równania u(x,y) = y(c+y), gdzie g{f) jest dowolną funkcją klasy C¹ w przedziale ( — *, +00).

Ponieważ u{0. /) => g(y) - y*. więc g(x+y) - (*+y)*, a zatem całką szczególną spełniającą dany warunek początkowy jest funkcja «(*, y) — <x+y)^ł.

Przykład 2. Znaleźć całkę szczególną równania u_xx = 0 określoną na całej płaszczyźnie i spełniającą warunki początkowe: u(0, y) — y*. a«<0, y) = y.

Całka ogólna tego równania u(x, y) - g(y)x+/i(y), gdzie siy) i *(y) są to dowolne funkcje klasy C‘ w przedziale (-os, -cc). Korzystając z warunków początkowych otrzymujemy :h(y) = y², g(y) •= y. Szukaną całką szczególną danego równania jest wiec funkcja u(x, y) — xy+y².

Powstaje pytanie, przy jakich założeniach o funkcjach występujących w równaniach (11.12) i (11.14) oraz o funkcjach występujących w warunkach początkowych (11.13) i (IMS) zagadnienie Cauchy’ego ma jednoznaczne rozwiązanie? Na pytanie to dają odpowiedź dwa twierdzenia, udowodnione przez wybitną matematyczkę rosyjską Zofię Kowalewską (1850-1891). Twierdzenia tc są znane w literaturze pod nazwą twierdzeń Cauchy’ego-Kowalew$kiej. Przed ich sformułowaniem wprowadzimy pojęcie funkcji analitycznej.

Def. Funkcję f(x) nazywamy analityczną w otoczeniu Q punktu x₀, jeżeli

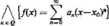
Wiadomo, że funkcja analityczna w otoczeniu Q punktu x₀ ma w tym otoczeniu pochodne dowolnego rzędu, a ponadto dla każdej liczby naturalnej n

Szereg (11.16) jest wówczas szeregiem Taylora funkcji f(x) (por. część II, rozdz. 111, p. 10).