00098467

150 U- RÓWNANIA KÓŻMIC7.KOWE CZĄSTKOWE

Na przykład funkcja f{x) — e" jest analityczna w dowolnym otoczeniu punktu x„ 0, po-

150 U- RÓWNANIA KÓŻMIC7.KOWE CZĄSTKOWE

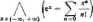
DcŁ Funkcję _/(*, y) nazywamy analityczną w otoczeniu Q punktu /'₀(x₀; >o). jeżeli

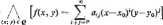
Można udowodnić, ie funkcja analityczna w otoczeniu Q punktu P₀ ma w tym otoczeniu pochodne cząstkowe dowolnego rzędu, a ponadto dla każdej pary (l,J) nieujemnych liczi całkowitych

1    d‘*'f(P₀)

^a‘^l njt dzfdyi

Szereg potęgowy dwóch zmiennych (11.17) jest wówczas szeregiem Taylora funkcji f(x,y).

Na przykład funkcja f(x, y) = sinfr+y) jest analityczna w dowolnym otoczeniu Q punktu (0; 0), ponieważ

V+J)*

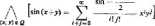
Podobnie definiujemy pojęcie funkcji analitycznej trzech lob większej liczby zmiennych niezależnych.

Podamy teraz bez dowodu zapowiedziane wcześniej dwa twierdzenia Cauchy’ego-Kowalewskiej odnoszące się odpowiednio do równania (11.12) oraz do równania (11.14).

Tw. 1. Jeteti:

\° funkcja    ,..., r₆) Jest analityczna w pewnym otoczeniu punktu (x₀;

r funkcja <p(y, z) Jest analityczna w pewnym otoczeniu punktu (y₀; z₀) e D\.

to istnieje otoczenie punktu (x₀; y>₀; z₀) e Z>,, w którym zagadnienie Cauch/ego dla równania (ILI2) ma dokładnie jedno rozwiązanie analityczne

Tw. 2. Jeteli:

\°funkcja    Jest analityczna w pewnym otoczeniu punktu

(jtoiTo;^; foi*®; —;*?«) gGj.

2“ funkcje tfĄy,z,t) i y(y,z, t) są analityczne w pewnym otoczeniu punktu O-o.Zo.toJeZżj,

to istnieje otoczenie punktu (*„; y_a; z„; t₀) e/),.w którym zagadnienie Cauchy’ego dla równania (II. 14) ma dokładnie jedno rozwiązanie analityczne.

WIADOMOŚCI WSTĘPNE

Uwaga. Niech będzie dane równanie różniczkowe cząstkowe rzędu pierwszego

r.

w którym u - «(.r. yj jest funkcją niewiadomą, a /(ei.Cj, vi.v,) jest funkcją daną ^oWBS w pewnym obszarze Sio £,.    oleg*

Zagadnienie Cauchycgo dla tego równania w prostokącie P:a < x < b, c < y '* " ^p na wyznaczeniu takiego rozwiązania u -* u(x, y), które spełnia warunek początkowy «(*□,>•) v(y)

przy czym liczba

az funkcja y(y) określona w przedziale <c, dy są z góry daj*-

nację geometryczną. Chodzi mianowicie o wyznaczenie ta całkowej u — u{x, v) danego równania, która przechodzi przez z góry daną krzyw*

r-x₀, o = f(y),    y«(c. d)

Bardzo często zagadnienie to formułuje się w ogólniejszej postaci. Chodzi wówczas enie powierzchni całkowej danego równania przechodzącej przez krzywą

tfl.lM

ar = *<»),    y-y(0.    «-*K0.    »e(i,»

która nic zawsze leży w jednej płaszczyźnie.    . .

Może się zdatzyć, że przez krzywą (11.18) lub (11.19) przechodzi nieskończenie wic* wierzchni całkowych równania. Krzywą taką nazywamy wówczas charakterystyką tego równa

ĆWICZENI A

1.    Jakie równanie nazywamy równaniem różniczkowym cząstkowym? Podać defintCN-a) rzędu, b) całki szczególną, c) całki ogólnej równania różniczkowego cząstkowego.

2.    Na czym polega zagadnienie Cauchy’ego: a) dla równania różniczkowego cząstkowego rzędu pierwszego, b) dla równania różniczkowego cząstkowego rzędu drugiego?

3.    Sformułować twierdzenia Cauchy’ego-Kowalewskiej dla równań (11.12) i (IM*)-

aa(ż-i-B) .

4. Wykazać, że funkcja u — p ary jest n

-Xy-n) --“0» dowolnym obszarze płaskim zawartym w zbiorze D - {(.?;y):.ry> 0).

5. Wykazać, że funkcja « — jest rozwiązaniem szczególnym rówr

w dowolnym obszarze płaskim zawartym w zbiorze D — {(z; y):y ^ 0}.

6- Znaleźć równanie różniczkowe o pochodnych cząstkowych rzędu pierwszego z funkcją niewiadomą u(x, y), klóre w dowolnym obszarze płaskim ma rozwiązanie postaci : a) u - /(*+>')4-+x~y, b) u =/(z^,-y^,)₁ gdzie/jest dowolną funkcją klasy C‘ w przedziale (-oo, -IM).

ćrr

ć pochodne — i —, a następnie z otrzymanych równań wyru-

Wskazówka. gować funkcję /•

7. Znaleźć równanie różniczkowe o pochodnych cząstkowych rzędu drugiego z funkcją niewiadomą n(x, <), które ma w dowolnym obszarze płaskim rozwiązanie postaci: al B-ZWsinr+^Wcos/, _b) .=/(*)*„, _c) u =/(,+rH»(x-r), gdzie f i _f s, (o do-wolne funkcje Masy C‘ w przedzale (~,»_t +«).