00098468

152 IŁ RÓWNANIA RÓŻNICZKOWO CZĄSTKOWE

& Znaleźć całkę szczególną równania u—x -—rt¹' "■ 0 w obszarze

152 IŁ RÓWNANIA RÓŻNICZKOWO CZĄSTKOWE

— —/*•

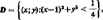
Wskazówka. Przyjmując y za parametr rozwiązać Janc równanie jako równanie różniczkowe zwyczajne.

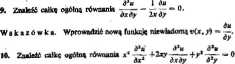
Wskazówka. Wprowadzić.

niezależne f

y

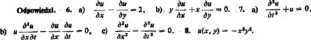
9. u(x, y) - /(z) /*+zM. «Jz>o/l» i /<*) u to funkcje dowolne klasy C‘; pierwsza w przedziale

• (-

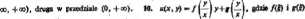
gą to dowolne funkcje klasy C* w przedziale (— co, +03).

2. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE LINIOWE I QUASI-LINIOWE RZĘDU PIERWSZEGO

Drf. Równanie różniczkowe cząstkowe

P(x. y.    y, z)    +.*(*, y,    y, *) (itw)

gdzie P(x, y, z), Q(x, y, z), S(x, y, z) i J{x, y, z) są danymi funkcjami klasy C‘ ^ pewnym obszarze D c B_a> nazywamy równaniem różniczkowym cząstkowym liniowym rzędu pierwszego z funkcją niewiadomą u ■= u{x, y, z).

Równanie (H.20) nazywamy jednorodnym, jeżeli flpt,y,z) s= 0 w obszarze D, niejednorodnym zaś w przypadku przeciwnym.

Zajmiemy sty równaniem jednorodnym

(D.21)

y. *>    +C(*. y.^z) +*(*. y.^)-^- = o

w którym co najmniej jedna z funkcji P(x,y, z), Q(x, y,z) i R(x, y, z) jest różna od zera w całym obszarze D.

Równanie (11.21) pozostaje w ścisłym związku z następującym układem równań różniczkowych zwyczajnych

__dx _ dy    dz

P(x, y, z) ~ Q(x, y, z) ~ X(x, y, z)

W dalszym ciągu zakładać będziemy, że P(x, y,z) # 0 w całym obszarze D. Wówczas zmienną x w układzie (11.22) możemy traktować jako zmienną niezależną, a pozostałe zmienne y i z jako jej funkcje.

Niech para funkcji

}<*). *(*)    OT.p)

będzie dowolnym rozwiązaniem układu (11.22). Wspomniany związek równania (1121) z układem (11.22) ustalają twierdzenia, które teraz podamy.

Tw. 1. Jeteli funkcja

u = z)    01.24)

Jest rozwiązaniem równania (11.21) w obszarze D, to funkcja

<!>(x,y,z)    (IL25)

jest całką pierwszą układu (11.22).

DOWÓD. Wstawiając (0.23) do (0.25) otrzynsmy funkcję złożoną tf>U, 2<*>, z(a)J, dó

ktÓRj pochodna wyraża uc wzorem

dy dx

dip dz_

•    dx

*

Wobec (11.22) i (0.26) m

+*(*. y,z) —

i w nawiasie prostokątnym równa ’■« » fiU. yW. *(*)! - const. Funkcja (025) Jcat <*»* P*™’**    ^cnd-

Tw. Ł Jeteli funkcja </.(*,/,*) klasy C‘ w obszarze O jest całką pierwszą układu (1122), to funkcja u = tf(x,y. z) jk« rozwiązaniem równania (H21).

DOWÓD. Ponieważ para funkcji y(x), «(*) Jmt rozwiązaniem układu (U-22). wi*

(tt	(0.27)
<Hp dy i<j> dz *iydx dt dx	(0.28)

X*). zWl - eonu. «k«ó

Z dru«iej strony