00098470

232 II RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE

ĆWICZENIA

1.    Podać definicje funkcjonale oraz definicje minimum i maksimum funkcjonału (11.245).

2.    Wypowiedzieć Iwieidzenia formułujące warunki konieczne dla ekstremum funkcjonału (11.245).

3.    Zbadać ekstremum funkcjonału

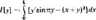
4.    Spośród wszystkich funkcji y — y(x) klasy C w przedziale <0, 1> o wykresach łączących punkty .4(0; I) i B(1; chi) wyznaczyć te. przy które; powierzchnia powstała z obrotu jej wykresu wokół osi Os ma najmniejsze pole.

Wskazówka. Po sprowadzeniu równania Eulera do równania różniczkowego rzędu pierwszego wprowadzić za pomocą podstawienia y' ■ shę nową funkcje niewiadomą <p ■= ${*).

5.    Wiadomo, że funkcja >•(*), dia której funkcjonał (II.24S) osiąga ekstremum przy wa-

(IŁ275)

J 4>(*. y, y")dx — const

jest całką równania Eulera dU funkcjonału

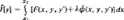
gdzie 2 jest pewną stalą. Stalą ż oraz stale całkowania wyznaczamy z warunku (11.275) i warunków brzegowych: y(x,) =■ y,, y(x,) - y_t.

Spośród wszystkich funkcji y — yfx) klasy C* w przedziale <• I, 1> o wykresach łączących

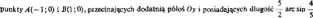
wyznaczyć te funkoe. której wykres wraz z odcinkiem AB ogranicza obszar o największym polu.

Wskazówka. Po jednokrotnym całkowaniu równania Eulera wprowadzić za pomocą podstawienia y" = tgr nową funkcje niewiadomą i = /(*).

FUNKCJE ZMIENNEJ ZESPOLONEJ 1. PŁASZCZYZNA ZESPOLONA OTWARTA I DOMKNIĘTA

O liczbach zespolonych była już mowa w trzecim tomie tego podręcznika. Pamiętamy, że liczba zespolona jest to para uporządkowana (x,y) liczb rzeczywistych x,y, przy czym równość, dodawanie i mnożenie liczb zespolonych są określone następująco:

Def. (x, y) = (u, t>) (x = u) a (y — v)

Def. (x, y)+ (u,»') = (x+u, y+v)

Def. (x, y) ■ (ii, t>) = (xu-yv, xv+yu)

Liczbę zespoloną (x, 0) utożsamiamy z liczbą rzeczywistą x:

(x, 0) ■= x    (Ul i)

Liczbę zespoloną (0, 1) nazywamy jednostką urojoną i oznaczamy literą j: (0,1) = /    (nt.J)

Łatwo sprawdzić, żc (0,1) - (0, 1) = (—1, 0). Biorąc pod uwagę równość (IIL1) i (III.2) oraz posługując się symbolem potęgi, mamy więc

1    (IU.3)

W dalszym ciągu będziemy zazwyczaj oznaczać liczbę zespoloną (x, y) jedną literą, np. z. Liczbę rzeczywistą x nazywamy przy tym częścią rzeczywistą, natomiast liczbę rzeczywistą y — częścią urojoną liczby zespolonej z = (x, y).

Używamy następujących oznaczeń:

x =- Rer oraz y = Im z

Symbole: Re oraz Im pochodzą od stów łacińskich reałis (rzeczywisty) oraz imagi-nurius (urojony).

Każdą liczbę zespoloną z — (x, y) można przedstawić w tzw. postaci kanonicznej (albo algebraicznej)

z = x+jy    '    (UL4)

liczby zespolone interpretujemy w znany sposób na płaszczyźnie prostokątnego, kartezjańskiego układu współrzędnych Oxy. Każdemu punktowi tej płaszczyzny F(x; y) jest przyporządkowana dokładnie jedna liczba zespolona (III.4)