00098471

234
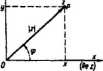
I na odwrót, każde) liczbie zespolonej (UI.4) jest przyporządkowany dokładnie jeden punki P(x;y) płaszczyzny. Utożsamiając punkty J*(x;y) rozważanej płmezyzny Z Herbami z — x+Jy mówimy, Ze jest to płaszczyzna liczbowa albo płaszczyzna zespolona (dokładniej: płaszczyzna zespolona otwarta); płaszczyznę tą oznaczać będziemy symbolem Z.
y
(fez) z
Rys. m.l
Odległość punktu z od punktu 0 (rys. III.I) nazywamy modułem liczby zespolonej z i oznaczamy symbolem |z|. Mamy więc
Niech r «t 0. Każdą liczbę rzeczywistą 4> spełniającą dwa warunki:
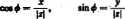
OLS)
nazywamy argumentem liczby zespolonej. Oczywiście, każda liczba zespolona (różna
od zera) nu nieskończenie wiele argumentów. Każde dwa spośród nich różnią się między sobą o całkowitą wielokrotność liczby 2n. Ten z argumentów, który należy do przedziału (—w, +it) nazywamy argumentem głównym i oznaczamy symbolem argz albo literą f. Argument główny jest określony jednoznacznie, co wynika z postaci warunków (III.5).
Zbiór wszystkich argumentów liczby zespolonej n> 0 omammy symbolem Argz i nazywamy argumentem wieloznacznym (krótko: argumentem). Elementy tego zbioru nazywamy wartobcimti argumentu wieloznacznego. Piszemy przy tym
łub krótko
Argx«argz+2w* (* ■* 0, ± 1, ± 2....)
4 — f>+2itk
mąjąc na myśli, że do zbioru Argz należą wszytkie te i tylko te liczby, które różnią się od argz o całkowitą wielokrotność 2n.
Zwracamy nwsąa i» sywbol Arg z oznacza nie jałną Hrabi leos Mór nksżeń^ria wMu ittb — nwwiąiai nUańn (HL3)—podotas idy arą * mwarra doUntais jedną liczbę » pnMrteła
<-*, +»>.
Argz można interpretować jako zbiór wszystkich miar lukowych kąta skierowanego wektora OP (ryt. ULI) z osią rzeczywistą. Argument główny q> stanowi tę miarę łukową tego kąta, która należy do przedziału (—ir, n>.
Uwaga. Odnośnie argumentu liczby zespolonej 0 można zajmować jedno z dłwSch itnno-wtsk: argument liczby 0 nie Jest określony albo (stanowisko bardziej wygodne) kałda liczba rzeczywista jest argumentem liczby 0. W tym drugim przypadku każdą liczbą z przedziału (—«, + »> można uwalać za argument główny liczby 0.
Pamiętamy, że każdą liczbę zespoloną (III.4) można zapisać w postaci trygonometrycznej
z= |r|(cos^-h/$in^) (in.6)
We wzorze tym można podstawić na miejsce 4> jakąkolwiek wartość Argz, na przykład argument główny.
Symbol |z[ modułu liczby z zastępujemy często jedną Hterą, na przy Wad r albo e-
leżeli i, i 2j tą dwiema różnymi od zera liczbami zespolonymi, to prawdziwe są następujące zależności:
moduł iloczynu równa się iloczynowi modułów
l»,**g|-l»il*W
moduł ilorazu równa tlą ilorazowi modułów
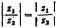
argument iloczynu równa tię su®5® grgumentów
Arg(z, • z*) - Arg z, 4 Arg *z 00.7)
argument ilorazu równa się bóżnicy argumentów
Arg — — Arg z, —Arg z, (ULI)
«i
Uwaga I. Równość (UL7) omami, la ifia każdej wirtoćd argumentu Arg (z, z») WaMŚ* taka wartośćennmmta Arg*, onu WaM# ■** włrto4ć<PJ argumentu Argz,. te -Ó>+Ó> Równość (OLI) należy rozumieć analogten*-Uwaga 2. Jetefi we wzorach (10.7) I <BLD *art«dw *yn*ole argumentu (Arg) rym-bolaml ugmeotćw tffrntycłi (an), to otrzymany równośd fiduywt. l*ot—, na
przykład z, - -I, z, - mamy
Wfr. rO-Bit-J)---, argz, -“+*'
•nu - *nJ~ +1*
Wyszukiwarka