00098473

238 IB. FUNKCJI ZMIENNEJ ZŁ1TOL0NBI

4. Czy równoii ) yf—\ określa liczbę / jednoznacznie T

9. Podać iotezpeetagt geometryczną modułu |r,-r,l, * następnie narysować ni płaszczyźnie ztspoknag zbiór punktów określony warunkiem:    •) |X-1| < 1.

b) 2 < lz+li < 3,    «) fx+IH-|z-II -4, d) |x+4l>3.

«. Obfayć:    I) /=T, b) y=T*7. c) ^-«+/*V3, d) yr.

7. Rozwiązać równań:    *) zT-Zr-f-J — 0, b) z*+4z+13 — 0,

C) Z*-l = 0, d) Z^+ttr¹ — 0.

*- Napisać postać trygonometryczną z irgumcnton fłównym liczby zespolonej:    •) 2+2/,

»~4>- «>³- «

9.    współrzędne (f, ij, Q rzutu stenograficznego P punktu z — x+iy ni sfer* Ricmanni (patrz ryv III2).

10.    Wykazać, że pierwiastki *»,*i fównłnia z* — 1 spełniają wirinek:

•) X, +*,+*, = 0, b) Z, z, z, - 1.

IŁ Obłkzyćzi/zrównania: 2+$#«-:yy- 14/+3jr—5/.

u. w,w.*    •* > N. pc^WU« .

\    2    | ⁺\    5    /    \—1, gdy 3 nie jest podoełrukiecn a

13. Uzasadnić poprawność względnie mepoprawność oastepu.ącye, równości -1 mp    „ /f- X) (-1) - /T - 1 .

Wskazówka. W dziedzinie zespotoacj pierwiastek alt jest jednoznaczny -

Odpowiedzi. 4. Nie; jednostka urojona / jezt tylko jśdaą z wartości /-^77 i Odkroić punktu z, od punktu z,; a) n(iin kola o środku 1 I promieniu I, b) wnętrze pfcrśdenia kołowego o środku -1 ( promieniach 2 13. c) elipsa u ogniskach -Ml oraz osi duląj 4, koła o środku -4 i promieniu ).«,•)/, -A

[eoa^-*+■£*)+/«,(£«+ j, k - 0, ł, 2, J,

.BL.il' . "Ml

■=> 2

2w*

co.—+/ńt—    1-0,1,2,3,4,3. 7. a) 1-2/. 1+2/. b> -2-2/.-2+V.

2. -1-//3.-H-Z^S; d) M->x. t. .) 2/f(co.l+/»to|),

' 7 [*"*(' t) ⁺^*^to(-y)]r C) J(coa0F/dn0). d) 2 Jcoa(-i«)+/*in(-|tf)]. -    , _ ¹ kizl    I ylf .    |ł|*

•^f    it-~rnzr- ^ia* * — 4.^ — 2.

1 CIĄGI I SZEREGI UCZBOWE O WYRAZACH ZESPOLONYCH

Rozwmtmy nąj nieskończony o wyrazach uspęionych

— ........

który oznaczać będziemy krótko iymboł*m

M

Ciu ten jest oczywiście funkcją, której riwdriną jest zbiór W, zaś przeciw dziadzi-W — pewien zbiór bob zespolonych.

Na rys. HL3 jot przedstawiona interpretacja geometryczna ciągu I —>.

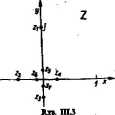
Określimy teraz granice (wfaieńwą) lim z, ciągu {z.}. Niech g = a+fb oznacza pewną liczb; zespoloną.

De#.    (Umz.'=:g)'»/\\//\lĄ,~gI<«    (ULU)

Ponieważ

K-g\=Vi^y+iy-^

przy czym X, = Rcr,, j, «= Im z,, wiąc łatwo zauważyć, że

(Km*. «*)■•► (lim*,-«) A (Umy, = b)    CHL1Z)

Jeżeli dąg {z.} ma granic; właściwą, to mówimy, że jest zbieżny. Ciąg, który nie ma granicy właściwej, nazywamy rozbieżnym.

W teorii dągów bczbowych o wyrazach zespolonych wprowadza się pojmie granicy niewłaściwej oo, mianowicie:

Drf. (lim«. = co)«-/\ V A W >** CHL13)

Uwaga Dla dąg&W Herbowych o wyrazach ra*CŁywktych. rorpatrup ń; dwie granico l_|Tlr<li... _(» ofit 4 o3,co jeaturaradojonetwukturązbioru M wwyitkich liczbraoczywntych. PiMZcazni liczbowa n» natomiast tylko jeden punkt w nieskoAcwnotó i dlatego dla ciągów o wynuacb aapotooych rotpatnjje »K tylko jedną grani* niewłaściwą: co.

Do ciągów o wyrazach zespolonych można stosować twierdzenia o działaniach giytBetycznych na granicach dągów zbieżnych, w brzmienia takim, jak dla ciągów o wyrazach rzeczywistych. Zwródmy jednsk w tym miejscu uwag; na to, te pewne pojęcia teorii ciągów, znane z podstaw rachunku różniczkowego funkcji jednej imiennej, nie mają w ogóle sensu dla dągów o wyrazach zespolonych. Na przykład nie ma okreflooego sensu pojecie ciągu mcmotonkanego, gdyż liczb zespolonych