00098481

254 m. FUNKCJE ZMIENNEJ ZESPOLONEJ

przy czym oflrżr) - o.tUlżO+yMidrl) j»t meskońocme małą r*du wytarto rui Lir . gdy Ufrt— 0. tzn.

<w    mus

.<*. -O Uf

Stąd

dw j ów <H-\    «0J<0

J» * l i* ** iz f ⁺ Ar

Sum* w nawaur po prawej Mionie t«j równoSci jot okreiloną bczh*. niezależną od ńt, natoatoaa drugi składnik dąż; do zen gdy Jr — 0, co jetl konsekwencją rówootd (III 441. Wynika stąd.

» granicą wtofciwą gdy dr— 0, a zatem/^-!*,) atskje I równa tią -

waga. Załntotue o rASraczkowalaodd funkcji «łs.y) i o(a.y) w punkcie    jm

ma i ctągkdu w otoczeniu punktu (a«; Pol pochodnych (OL4I i. natwmaat jeat slbiitfzzz od ałarccia ctągłoici funkcji /(z) w po-ikoe r« Wynika stąd, Ze jeżek funkcja «<», y) i tHx, ył są klaty O » pewnym otocraniu punktu (*•; y«). a ponadto w punkcie lym apeinione •ą warunki Cmciy    to pochodna/"(r.) istnieje Nie wynika stąd natomiast, to dągkóć

funkcji Ąj) w punkcie t, oaz spełnienit w tym punkcie warunków Ciuchy'ego- Kkmanna zapewnia łatnwme pochodnej/*(>•) Udowodniono jednak, to jeteli funkcja /(*) jaat ciągła w pewnym ohumzt i spełnia w nim warunki Ćnuc b y *c go-R I arna a o a, i o iitnieje pochodna /*(*( • każdym punkcie tego ohazgrn. Tao ostatni warunek wyauitzajwry. który dotyczy ntcietua pochodnej /"(*) » pewnym obiuou. jat hardao prasty. judnakto je#> dowód wykracza znacznie poza ramy tego podtącamka.

PtoyUai. Razawutray fonkdeftil - •*.czyli

/(r)- e*cea»i-/e*llny

Fonkzje ■<«. ył i «(*. y) są ta kiaay C« aa c»lą> ptoaeczyźnia. a ponadto

da    dv

—-e*«st»y.    —    -    -*»sloy

do    do

57—'

Więc warunki CaaeMy tto- flarunawag tą tpełaioM. Wynika stąd, la mpatrywana funkcja aa w każdym punkcie z. płaszczymy pochodną /“(*#) ^T« pochodną można obliczy* na przykład a poił (U1.1S)

f(u) — «*• a* r.+/ «in y»

rM - e«a Vh, czyli A/,) - t*«

Nazwa wortmkl Cauchy'ego-Riemcmrui, którą wprowadziliśmy dla równości (UL40), nie mg urasacfjiienia historycznego. Warunki te znane jut były w XVIII w. d'AuwtTOwi i Eulzbowi, a więc nie tylko na wiele lat przed urodzeniem Rre-MANNA, ale także przed urodzeniem Cauchv'eoo Zasługą CauchY KK) i Rlfi-manna jest jednakie precyzyjne zbudowanie pod naw współczesnej teorii funkcji zmiennej zespolonej i z tego względu ich nazwiska związano z równościami (111.40), które mają dla tej teorii podstawowe znaczeni!. Należy zaznaczyć, te warunki (111.40) pojawiły się po raz pierwszy w łych pracach d'AIemberta ł Eulera, które dotyczyły zagadnień hydromechaniki.

ObHoaale pocfcodae] f(a). Omówimy teraz w krótkim zarysie (pomijając dowody) obliczanie pochodnej funkcji zmiennej zespolonej. Wzory i twierdzenia, jakie przy tym podamy, mają dobrze znane odpowiedniki w rachunku różniczkowym funkcji jednej zmiennej rzeczywistej. Fakt ten wynika stąd, że definicja (IIL35) ma taką samą postać jak definicja pochodnej funkcji zmiennej rzeczywistej.

Na wstąpię wprowadzimy nowy, bardziej dogodny w wielu wzorach symbol pochodnej, mianowicie

który będziemy używali na równi z symbolem /'(z).

Przechodzimy teraz do podania kilku podstawowych wzorów i twierdzeń.

Pochodna funkcji stałej JU)~e jest równa zeru

f(z) « 0

Pochodna funkcji potęgowej flz) = z*, wyraża się wzorem

A*)-"**'¹

Litera n oznacza tu dowolną liczbę naturalną, mykiaj

/« - 3+v. rw - o, m - **. ru) - a**

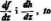
Tw. (o działaniach arytmetycznych na pochodnych). Jeteli tinitją pofhodn*

_AWz)+*(z)l«= ^ +

^Wr) •*<*)] = ^ - *(*)+ ^ /W

ortu, przy dodatkowym zahtmiu A(z) * 0

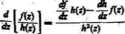
/(*) 4. »+,*, /._w _ 1+31*.    *(*) - Jł*

2*-IO*    ¹    _ ^0,-11 .

FM-

? **

(Zł*⁰)