00098484

260 m. FUNKCJE ZMIENNEJ ZESPOLONEJ j
WŃC OSUlecznie
A oznacza lu óowotna uałą *rofo*q. «lór» stanom wartutć funkcji /<j) w początku układu,
A -/<0).
,W podobny sposób znajduje się funkcję holomorficzny /(z), gdy dana jest jąj' część urojona. Odpowiednikiem wzoru (111.49) jest wówczas wzór
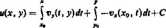
P-W)
Interpretacja geometryczna. Rozważmy funkcję holomorficzną Az) = >)+ :
+MX>P) różną od stałej i utwórzmy dwa pola wektorowe
P = grad uf*, y) oraz Q — grad c(jc, y)
Ponieważ iloczyn skalarny P ■ Q — 0, gdyż z uwagi na warunki Cauchy'ego-Rie* manna mamy
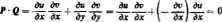
więc wektor p jest ortogonalny do wektora Q w każdym punkcie rozpatrywanego obszaru. Wynika stąd, że rodziny linii
u(x, y) — const oraz tt(x, y) — const są ortogonalne jedna względem drugiej (rys. II 1.7).
y
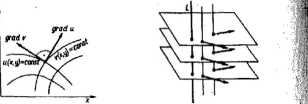
Rys. 111.7
Rys. 111.9
o
Na przykład rodzina linii x,-y> - consi jen orlo«onaln« do rodziny linii 2xy - const, gdyż funkcja x>~y> ty2rv, czyli z*, jest holomorficzna.
Interpretacja elektrostatyczna. Rozważmy prostą L pokrytą ładunkiem elektrycznym o stałej gęstości liniowej q. Ładunek len wytwarza pole elekłrosta* tyczne plasko-rówrtolegle. Wektory tego pola zaczepiane w dowolnych punktach jednej prostej, równoległej do prostej L, tą równe (ry*. HI.8). Dla poznania właściwości pola płasko-równoleglego wystarczy więc dokonać analizy w jednej z ptaszę czyzn prostopadłych do prostej L. Pole elektrostatyczne okreilone w takiej płaszczyźnie nazywamy płaskim polem elektrostatycznym.
Wybierzmy jedną z płaszczyzn prostopadłych do prostej L. ustalmy na niej prostokątny, kartezjański układ współrzędnych Oxy (rys. 111.9) i traktujmy ją jako płaszczyznę zespoloną Z. Odcinek dl prostej L wytwarza pole elektrostatyczne. Rzut wektora tego poła w punkcie z na płaszczyznę Z wynosi w przybliżenia
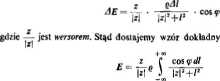
l
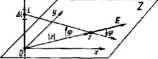
Rvs. m.9
Wprowadzamy nową zmienną całkowania f. Mamy
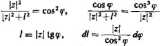
Ody /rośnie od — 00 do -ł-ce, to <p rośnie od —do + Mamy zatem
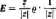
J cosifd<p
czyli
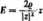
(111.52)
Wartość natężenia E rozważanego płaskiego pola elektrostatycznego można więc zapisać za pomocą Funkcji zmiennej zespolonej w postaci (III.32) bądź też, oddzielając część rzeczywistą od części urojonej, w postaci
Wyszukiwarka