00098488

266 III- FUNKCJE ZMIENNEJ ZŁSFOŁONEJ

Wyrazy ciągu (111.62) nazywamy sumami cZfSciowymi szeregu (111.63), natomiast funkcje/,(z),/,(i),, nazywamy wyrazami tego szeregu.

Def. Szereg (111.63) zbieżny w zbiorze f! nazywamy bezwzględnie zbietnym w tym zbiorze, jeżeli dla każdego z € SI zbieżny jest szereg

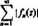
OHM)

Można udowodni, że zbieżno! i szeregu (111.64) zapewnia zbieżność szeregu (111.63) w tym samym zbiorze.

!

Kryteriom Wcicrstnma. Jeteli dla kat de go ne N i dla kaidego z e Ci Jest

mona nierówność |/.(z)| < a., przy ctym szereg liczbowy £ o, jest zbieżny, W szereg £/.(z) zbitiny w zbiorze H Jednostajnie i bezwzględnie.

DOWÓD icao kryterium pominiemy, fdyt jest on bardzo podobny do dowodu kryterium o tej mwj nazwie odnoszącego sią do ciąiu funkgi zmienne) rzeczywista} (eze*ć II teąo podręcznik*, nadz. III, p. 7).

Szereg potęgowy Def. Szereg funkcyjny

on/

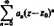
a_#+fl_ł(z-ze)+«j(z-z₀)^,+ - -ffl,(z'-ro)^,+ ...

dane, natomiast z jest zmienną.

Zajmiemy się bliżej strukturą zbioru Sio wszystkich wartości liczbowych zmiennej r. dla których szereg (iU.65) jest zbieżny.

Utwórzmy zbiór X liczb rzeczywistych, do którego zaliczymy wszystkie liczby U-Zol gdy z efto i tylko takie. liczby. Zbiór X jest więc zbiorem długości wszystkich odcinków o wspólnym początku r₀ i końcach reSl_Cl nie wykluczając przypadku z = Xo. który świadczy o tym, że zbiór X nie jest pusty.

Zbiór Xjeat ograniczony albo nieograniczony.

Def. Promień zbiełnoici R szeregu (111.65) jest to kres górny zbioru X.

Nie wykluczamy tu przypadku R ■= +ro.

Definicją promienia zbieżności szeregu (II 1.65) można też zanotować tak:

Prowadząc rozumowanie analogiczne do tego, które podaliśmy dla szeregów potęgowych zmiennej rzeczywistej (część H tego podręcznika, rozdz. UJ, p. 9), dochodzimy do następujących wniosków, dotyczących struktury zbioru il₀: l^a jeżeli R = 0, to szereg (III.65) jest zbieżny tylko dla z =- z₀,

2° jeżeli i? =+oo, to szereg 011.65) jest z b ie żny bezwzględnie dla każdego z (na całej płaszczyźnie otwartej),

3° jeżeli 0 < R < +eo, to szereg (111.65) jest zbieżny bezwzględnie dla ]z— r₀| < R, natomiast jest rozbieżny dla |z—z₀l > R; w punktach okręgu |z—z„| - R szereg (III.65) może być zarówno zbieżny jak i rozbieżny.

Koto o środku z₀ i promieniu R nazywamy kołem zbieinoici szeregu (111,65), W przypadku R 0, kolo to wyrodnieje do punktu, natomiast w drugim przypadku krańcowym, gdy R = +co, kołem zbieżności stąje się cala płaszczyzna. Przypadki 1°, 2°, 3° są przedstawione schematycznie na rys. 111,10.

Rys. 111.10

Zajmiemy ślę teraz znajdowaniem promienia zbieżności R szeregu potęgowego (111.65). Z podanych tu właściwości l°-3° wynika, że promień zbieżności szeregu (111.65) jest zarazem promieniem zbieżności szeregu

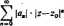
(111.67)

a więc szeregu potęgowego zmiennej rzeczywistej |z-r₀| o współczynnikach rzeczywistych jaj. Do badania szeregu (DI.67) możemy więc użyć metod poznanych w części II tego podręcznika (rozdz. tH, p. 9). Wynika stąd, że jeżeli istnieje granica (właściwa albo niewłaściwa)

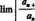
(111.68)

to

0, gdy 1 = +oo

*= -i,    gdy    0 < 1 < +oo

+00,    gdy    1=0

(01.69)