00098495

278 III. FUNKCJE ZMIENNEJ ZESPOLONEJ

więc funkcje wieloznaczne Lnz i Argr są ze sobą blisko spokrewnione. Ustalając | we wzorze (III.84) wartość k i ograniczając dziedzinę funkcji Lnr do zbioru A (patrz rys. 111.13), otrzymamy jednoznaczną i ciągłą gałąź funkcji wieli Lnz.

Przykładem takiej (altu jest funkcja

w = Id; (logarytm główny)

określona w zbiorze A.

Obszar A (rys. 111.13), w którym wydzielaliśmy gałęzie funkcji wieloznacznej Lnz nie jest jedynym, który się do tego celu nadaje. Można tu wziąć każdy obszar, który nie zawiera żadnej krzywej lordana mieszczącej w swym wnętrzu punkt 2=0. Punkt Ipn nazywamy punktem rozgałęzienia funkcji wieloznacznej Lnz.

■V»

Przykład. Wydzielić w półpłaszezyinie Re z < 0 galąi /(z) funkcji wieloznacznej Lnz w ten sposób, żeby/(—1) — 3mj.

Bierzemy pod uwagę wzór (IU.S4), Dla Re; < 0 i Im z > 0 lirabc k dobierzemy tak. żeby spełniony był postawiony w zadaniu warunek/(—I) *» 3itj. Mamy więc 37ty = 0+jO+ŻA)

czyli k - I. Dla Rez < 0 i Imz > 0 mamy żalem /(z) - Inr+Żrtj. W celu zapewnienia ciągłości funkcji /(z) na ujemnej pólosi, przyjmiemy dla Rez < 0 i Imz < 0,/(z) ™ lnz+4n/, gdyż wartość -lnz doznaje na tej półosi skoku o 2nj. Ostatecznie

flnx+2it/    dla Ra; < 0,

^ (lnj+4s/    dla Rez < 0

Podane dotychczas wiadomości odnośnie funkcji wieloznacznych oraz ich gałęzi stanowią skromną, lecz wystarczającą podstawę do przedstawienia śmiałej koncepcji geometrycznej Riemanna, która prowadzi do tzw. powierzchni Riemanna. Myślą przewodnią tej koncepcji było takie zmodyfikowanie pojęcia dziedziny funkcji wieloznacznej, które pozwoli traktować ją tak, jak funkcję Ą jednoznaczną.    -

Wyjaśnimy to na przykładzie funkcji wieloznacznej w — Lnr.

Dla każdej wartości z ? 0 funkcja U ma przeliczalnie wiele wartości lnz+/2rtik

k = 0, ±1, ±2,.... Każdej wartości całkowitej k przyporządkujemy płaszczyznę Zespoloną Z,, rozciętą wzdłuż ujemnej półosi: Rez* < 0, Imz, = 0.

Zaapelujmy teraz do naiwnego realizmu i wyobraźmy tobie, że dla każdego całkowitego k górny brzeg rozcięcia płaszczyzny o numerze k odpowiednio wyginamy i łączymy z dolnym brzegiem rozcięcia płaszczyzny o numerze k-fl (rys. III. 15), przy czym tylko płaszczyzny o sąsiednich numerach są w ten sposób połączone.

W tym miejscu widać, że realizm do którego apelujemy, musi być rzeczywiście naiwny, gdyż w przestrzeni trójwymiarowej Euklidesa taki układ płaszczyzn nie jest możliwy. Nie chodzi nam jednak o wyobrażenie sobie takiego układu płaszczyzn w przestrzeni E₃, lecz o ustalenie pewnych jego właściwości. Chodzi mianowicie o to, żeby punkt poruszający się po płaszczyźnie fc-tej znalazł się po przecięciu jej ujemnej półosi rzeczywistej na płaszczyźnie (*+ l)-szej, jeżeli przecięcie nastąpiło od strony Imz* > 0, natomiast na płaszczyźnie (fc -l)-szej. jeżeli przecięcie nastąpiło od strony Imz_t < 0. Mamy więc tu ściśle sprecyzowany przepis na przecinanie ujemnej półosi rzeczywistej, wobec którego naiwność realizmu związanego z wyobrażeniem sobie łączenia brzegów porozcinanych płaszczyzn nie jest sprawą istotną.

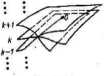
Rys. HI. 15

Opisany tu układ płaszczyzn nazywamy powierzchnią Riemanna funkcji Lnz. Powierzchnia ta zbudowana jest tak, że funkcja Lnz jest na niej jednoznaczna i ciągła. Jednoznaczność wynika stąd, że każda z płaszczyzn Z* — zwanych piatami powierzchni Riemanna, ma swój numer k, który determinuje poprzez równość (111.84) dokładnie jedną wartość Lni. Ciągłość wynika natomiast z przepisu dotyczącego przecinania ujemnych półosi rzeczywistych, który niweluje skok argumentu głównego.

Następujący przykład wyjaśnia naturalność pojęcia powierzchni Riemanna. Spójrzmy na zegarek i weźmy pod uwagę wskazówkę minutową. W ciągu godziny wykonuje ona obrót o 360°. Położenie tej wskazówki nie określa jednoznacznie chwili /, w której spojrzeliśmy na nią; może to być którakolwiek z chwil odległych od t o całkowitą wielokrotność godziny. W praktyce pomagamy sobie patrząc na wskazówkę godzinową. Jednemu położeniu wskazówki minutowej odpowiada wiele (przeliczalnie wiele) chwil, przy czym następują one w ustalonym porządku. Krążenie wskazówki minutowej jest więc jakby wodzeniem po powierzchni zbudowanej z przeliczalnie wielu tarcz zegarowych, odpowiednio rozciętych radialnie i złączonych brzegami, z których każda odpowiada dokładnie jednej godzinie. Położenie wskazówki minutowej na takiej powierzchni wyznacza chwilę i jednoznacznie. Naturalny jest tu zarazem przepis dotyczący przechodzenia przez złączenia brzegów: posuwając się zgodnie z ruchem wskazówki zegara, przechodzimy z tarczy o numerze k na taren o numerze fc+1, co wiąże aę bezpośrednio z ciągłością zmiany czasu.

A oto jeszcze jeden przykład. Rozważmy zależność

w™ }/z dla z* 0    (IIM

Jest to przykład funkcji dwuznacznej. Każdej wartości z * 0 funkcja ta przyporządk w uje dokładnie dwie wartości /z, mianowicie