00098496

280

. 'Sp

in rtiNKUc zuilnnlj /u.polonu

k «= 0.1 (JsljlajiłL wartość k otrzymamy funkcję jednoznaczną w obszarze 0 •    x. ale nieciągłą na ujemnej półosi rzeczywistej, i uwagi na nieciągłość

atg r. Wydzielenie gałęzi funkcji dwuznacznej (111.86) jest możliwe w odpowiednio zawężonej dziedzinie. r.p. w obszarze A (patrz rys. 111.13). Nu r.s. III 16 przcdsU-w;ono odwzorowaniu tego właśnie obszaru A za pomost dwóch gałęzi funkcji (111.86), mianowicie

h = |/Ż (fc - 0) oraz i. - , 1- (i I)

Oczywiście dla każdego z mamy

o' "^l/

III		■/>W/ m
		w
IMS	Ml Ms ip
	^ li Mili' Rys. IH.16

Dla funkcji (111.86) łatwo jest zbudować powierzchnię Riemanna. W tym celu wystarczy wziąć dwie płaszczyzny zespolone, oznaczyć jedną cyfrą 0, drugą cyfrą 1, następiuc rozdąć je wzdłuż ujemnej półosi rzeczywistej i złączyć brzeg górny cięcia na płaszczyźnie 0 z brzegiem dolnym cięcia na płaszczyźnie I, oraz brzeg górny cięcia na płaszczyźnie 1 z brzegiem dolnym cięcia na płaszczyźnie 0. Dwie pozostałe pary brzegów nie mogą mieć natomiast punklów wspólnych. Każdemu punktowi z płaszczyzny 0 przyporządkowujemy liczbę \/z, każdemu zaś punktowi z płaszczyzny 1 — liczbę \'z. Komentarz do budowy takiego układu płaszczyzn (układ ten Sianowi

powierzchnię Riemanna funkcji (III.86)) jest podobny jak w przypadku funkcji I Lnz. Chodzi tu nic o wyobrażenie sobie takiej powierzchni w przestrzeni E_}, co | nie jest możliwe, lecz o ustalenie przepisu dotyczącego przecinania ujemnej półosi rzeczywistej. Na tak zbudowanej powierzchni Riemanna funkcja w = j/r jest jednoznaczna i ciągła. Jednoznaczność jest tu oczywista, natomiast dągłość jest związana zc sposobem łączenia brzegów dwóch płaszczyzn (rys. III. 17) i z okresowością funkcji wykładniczej zmiennej zespolonej.

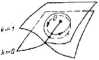
RYS. III.17

ĆWICZENIA

1. Podać definicję okresowości funkcji zmiennej zespolonej. Omówić interpretację genme-ryczną. Wyjaśnić dlaczego funkcja c' jest okresowa i podać kilka różnych jej okresów.

i. Podać definicję logarytmu naturalnego liczby zespolonej. Co to jest logaiytni główny? Omówić obliczanie logarytmów.

3.    Wykazać, że jeżeli Zjij ^ 0, to:

a) Łn(z,zj)—Lnii + Lnzj, b) Ln — Litr, -Lnzj

natomiast takie same wzory dlii logarytmów głównych są fałszywe (por. p. 1 tego rozdz., wzory (111.7) i (111.8)).

4.    Obliczyć:    a) Lne, b) lne, c) Ln( 1—yV^5>, d) ln(-l Ijj⁷?),

e) Ln(l-y), f) ln(I-j), g) Ln-™-.    1.) In--.

5.    Potęgę zespoloną liczby zespolone} o ł* O określamy następująco:    o* e^kL"

Potęga zespolona nie jest więc określona jednoznacznie. Liczbę e^Mra nazywamy wartością główną potęgi a».

Obliczyć:    a) }}, b) wartość główna }>, c) (-l)ż. d) wartość główną (-1)7.

6.    Jeżeli:

sinw = z    cos w = z    Iga — z    ctgw = z    (A)

to zależność wódz oznaczamy odpowiednio symbolem:

w — Aresinz    w = Arecosz    w = Are tg z    w *= Arcctgz

Zależności te są funkcjami nieskończenie wieloznacznymi, które nazywamy odpowiednio : aronem    arcusem    arcusem    aronem

sinusem    kosinasem    tangensem    kolongensrm

Wyprowadzić wzory:

a) Arcsinr — —/Ln(/z+l/!— z¹),    b) Arccosr —-/Lnfz+yp^-T),

c) Arctgz — Ln    d) Arcctgz — -i- Ln——

V I ~jz    2/ jz+t

Odpowiedzi sprawdzić, podstawiając je do odpowiedniej z równości (A).

7.    Obliczyć:    u) Arcsin/, b) Arctg2y, c) Arcsia2, d) Arctg(-I).

8.    Jeżeli:

shw “ 7    chw=2    tgw = z    ethw = •

Artltz

Arcthz

to zależność w od z oznaczamy odpowiednio symbolem w = Arehz w = Archi