00098498

284 Ul- FUNKCJE ZMIENNEJ ZESPOLONEJ
284 Ul- FUNKCJE ZMIENNEJ ZESPOLONEJ
rze D, to w jego obrazie — obszarze D’ —jest określona funkcja odwrotna z *» która jest także holomorficzna i jednokrotna w obszarze D', przy czym

równość (Ul,*7) w ten sposób
< fi**
Zwróćmy uwagę, « funkcją odwrotną względem (IB. (logarytm główny). Zgodnie z tym co powiedzieliśmy wyże] i jednokrotna w obsorae ŻV, przy czym
(por. wzór (111.47)).
Dowody tych właściwości funkcji jednokrotnych pominiemy. Przykład. Rozważmy funkcje
Wykażemy, że funkcja ta jest jednokrotna w obszarze
D: —oo <Rez< +®, —it<Imz<+it
Istotnie, równość e»> — e*» jest równoważna równości «*•“*» - I, ta z kolei
|w| tl‘'i*.('ełi
przy czym * — x+/j". Ponieważ ze O, wiec — n <y < + *. a zatem W**e» oraz argw-r
Biorąc pod uwagę zmienność x --zauważyć, że
0 < |w| < oo oraz -*-f ar*1* < +*
Obrazem D' obszaru D jest wiec cab płaszczyzna liczbowa bez ujemnej pób my 0). Rys. fn.18 przedstawia interpretacje geometryczną tego przykładu.
Uwaga. Funkcja (111.87) jest oczywiście jednokrotna w każdym obszarze, który zawiera się w pasie nieskończonym (111.88), a także w każdym pasie
—oo < Rez < + ao, a < Im z < b
jeżeli 0 < b—a < 2». Na przykład dla a = *, b ■= 3n obrazem obszaru — pasa w przekształceniu OH-87) będzie, tak jak poprzednio, obszar D' z rys. 111-18, jednakże funkcją odwrotną będzie tu nie z = In w, lecz z - law+2xj.
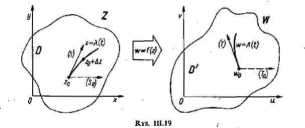
Niech/(z) będzie funkcją holomorficzną i jednokrotną w obszarze D, przy czym obraz tego obszaru w przekształceniu w =/(z) oznaczamy symbolem D' (rys. III. 19). W obszarze D wybieramy dowolnie punkt z0 e D i wyprowadzamy z tego punktu otwarty luk zwykły o równaniu
Z=^(f), 16 <«,/!> (UI.S9)
przy czym i(a) •= :0. Zakładamy przy tym, ie istnieje pochodna prawostronna A'(a+) # 0, co zapewnia istnienie jednostronnej stycznej do hiku (III.89) w punkcie zc. Odwzorowanie w *=J{z) przekształca łuk flll.89) na otwarty łuk zwykły w =» A(t), <nt.90)
przy czym -d(a) = flz0) = w,.
Wykażemy, że istnieje różna od zera pochodna prawostronna /l'(«+). Rozważmy dodatni przyrost Al parametru I taki, te a+At < fi, utwórzmy iloraz różnicowy
AA A{tt+At)—A(u)
At a At
i przekształćmy go następująco
AA flM*+At)l-ftM*J] /(z,+di)-/fa) Az At At Az ' At
gdzie Az = A(ct+d/)- A(«). Zauważmy, i zwykły. Stąd
Az s* 0, ponieważ łuk (IU.89) jest
A-(a+) -/-(*<,) W) (HI.91)
Wyszukiwarka