00098501

290

290

1

(IIL94)<

realizuje odwzotowanie rwane inwersją, przy czym obrazem punktu z — 0 ja* 'f w = co i na odwrót. Odwzorowanie to jest jednokrotne na całej płaszczyźnie . Gaussa. Funkcja (TI1.94) jest holotnorficzra na całej płaszczyźnie z wyjątkiem pOOr, ’. kiu z = 0 Inwersja odwzorowuje konforemnie całą płaszczyzny Gaussa ca sama. gdyż zachowuje ponacto kąt skierowany między każdymi dwoma kierunkami; ~ wyprowadzonymi z punktu 0 albo co.

Funkcję (HI.94) moZna traktować jako złożenie następujących odwzorowań:

Pierwsze z tych odwzorowań, to przekształcenie przez promienie odwrotne, i miast drugie jett symetrią względem csi rzeczyrństej.

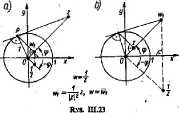
Na rys. III.23 jest przedstawiona konstrukcja, na podstawie której znając punkt z (różny od 0 i od eo) można znaleźć jego obraz w odwzorowaniu (111.94).. Rysunek tll.23a dotyczy przypadku, gdy j*| t* 1. Jeżeli |x| = 1. to odwzorowanie ; przez promienie odwrotne jest po prostu przekształceniem tożsamościowym, więo. inwersja (1X1,94) ogranicza aię do symetrii względem osi rzeczywistej. Jeżeli 0 < |z < 1, to obraz punktu z w inwersji (111.94) znajdujemy / konstrukcji przedstawionej Da rys. III.23b.

Odwzorowanie (111.94) przekształca wzajemnie jednor.ruiLZ.nie obszar |«| < 1 ,(tzw. koło jednostkowe) na obszar |w| > 1, do którego należy punkt w nieskończoności.

Inwersja ma dokładnie dwa punkty niezmiennicze, które znajdujemy z warunku

1 . , . . '

z = —, mianowicie z, — — 1 »*-,=* 1.

Homografia- Omawiana ostatnio inwersja należy do ważnej w zastosowaniach klasy odwzorowań homograficznych. Są to odwzorowania postaci

» - "I*    (HOT

cz+d

przy czym a, h, c i d oznaczają liczby zespolone spełniające warunek

H“ 3’^,i>

Jeżeli a = d=Ó i b = c = \, to homografia (UI.9S) jest inwersją (111.94), jeżeli natomiast c — 0, to homografia ta jest funkcją pierwszego stopnia.

Omówimy niektóre właściwości przekształcenia (10.95). Obrazem punktu </

* “5 ——w tym przekształceniu jest punkt w nieskończoności Jeżeli c 0 (tzw.

homografia wlaiciwa), to dzieląc az+b przez ci+d można równość (111.95) zapisać następująco

^⁵⁼¹ c cz+d ⁺T

Z równości tej wynika, że homografia właściwa jest superpozycją następujących odwzorowań:

r	w, = cz+d
2°	1 *1 = ~	(m.96)
	—& a
3®	*‘+T .

a więc jest superpozycją funkcji pierwszego stopnia, inwersji i ponownie funkcji pierwszego stopnia. Ponieważ każde z tych odwzorowań przekształca konforemnie płaszczyznę Gaussa na płaszczyznę Gaussa, więc tę samą właściwość ma odwzorowanie homograficzne.

B:    0 < Rez < +eo.

więc pierwsze z odwzorować (tjl.96) jest totaroośóowe, drogie jest inwersją, trsecie natomiast jest postaci w — -»»+!. Na rys. ni.24 przedsuwiono rozwiązanie tego przykładu.