00098503

UL FUNKCJE ZMIENNEJ ZESFOLONEJ

Ustalmy z kolei ? e (—«, +«>, natomiast r niech rośnie od 0 do 1. \ tej odpowiada oczywiście ruch punktu z po odcinku od punktu 0 do punktu co»'f% +/M?.

Rozpatrzmy kilka przypadków.

Jeżeli ? = —-y. to równania (III.99) są postaci u = 0

4(H

a więc punkt w porusza się po półprostej Rew = 0 i Łmw 0, od cc do 0. Jeżefi ? ■= -f—, to równania (10.99) są postaci Wc=0

•—t(H

a zatem punkt w porusza się po półprostej Rew = 0 i Imw ^ 0, od co do 0. , Podobnie dowodzimy, że dla f = 0 punkt w porusza się po półprostej Imw« i Rew > 1, od oo do 1, natomiast dla ? = w punkt w porusza się po Imw = 0 i Rew < —1, od punktu co do —1.

Pozostał jeszcze przypadek sin ? »* Oi cos? ¥• 0. Z uwagi na zależności (UL mamy wówczas

cos¹?

1-j— «= 1

(CL

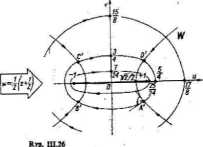
Jest to równanie hiperboli o półosi rzeczywistej |coi?| i- pół osi urojonej Na podstawie równań (III.99) łatwo jest zauważyć, że obrazem odcinka «: od punktu 0 do punktu cos? I-/sin? jest w tym przypadku część hiperboli o niu (IIL100), przebiegająca w odpowiedniej ćwiartce płaszczyzny W.

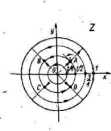
Rys. in.26 ilustruje przeprowadzone ostatnio rozważania. Zwracamy przy uwagę, że ortogonahtośi Unii rodziny aigz •= const do rodziny okręgów |t| => w przekształcanym kole |z| < I przenosi się—zgodnie z podanymi ; właściwościami odwzorowania konforemnego — na obrazy tych linii u 7—-™ przekształconym.

Fnkcja sin;. Zbadamy odwzorowanie za pomocą funkcji w = slnż

Ponieważ

(por. zad. 6, p. 7 tego rozdz.), więc funkcję sin z można uważać za superpozycję następujących czterech przekształceń:

w, -/z w_t ■= e^w‘

W, = -Jw₂

1*

2'

3“

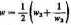
⁴°

Każde z tych czterech odwzorowań jest nam znane: pierwsze i trzecie są funkcjami pierwszego stbpnia stanowiącymi obroty, drugie jest funkcją wykładniczą, czwarte natomiast jest funkcją Żukowskiego. Ponieważ funkcja pierwszego stopnia jest jednokrotna na całej płaszczyźnie, więc badając jednokrotność funkcji sinz, wystarczy zbadać jednokrotność odwzorowań 2° i 4°.

Zaczniemy od odwzorowania 2°. Wiemy, że funkcja w₂ = e”¹ jest jednokrotna w pewnym obszarze wtedy i tylko wtedy, gdy dla każdych dwóch (różnych) punktóv wl i wi' z tego obszaru oraz dla każdej liczby całkowitej k jest spełniony warunel wi-wś' * 2irfgr

Oznaczając (por. 1”) wj —/z,, w" *=jz_lt dostajemy stąd warunek

Zj— Zi * 2itk    (UL 102)

Przejdźmy teraz do odwzorowania 4“. Wiemy, że funkcja Żukowskiego będąca tym odwzorowaniem jest jednokrotna w pewnym obszarze wtedy i tylko wtedy,