00098519

I. FUNKCJE ZMIENNEJ ZESPOLONE)

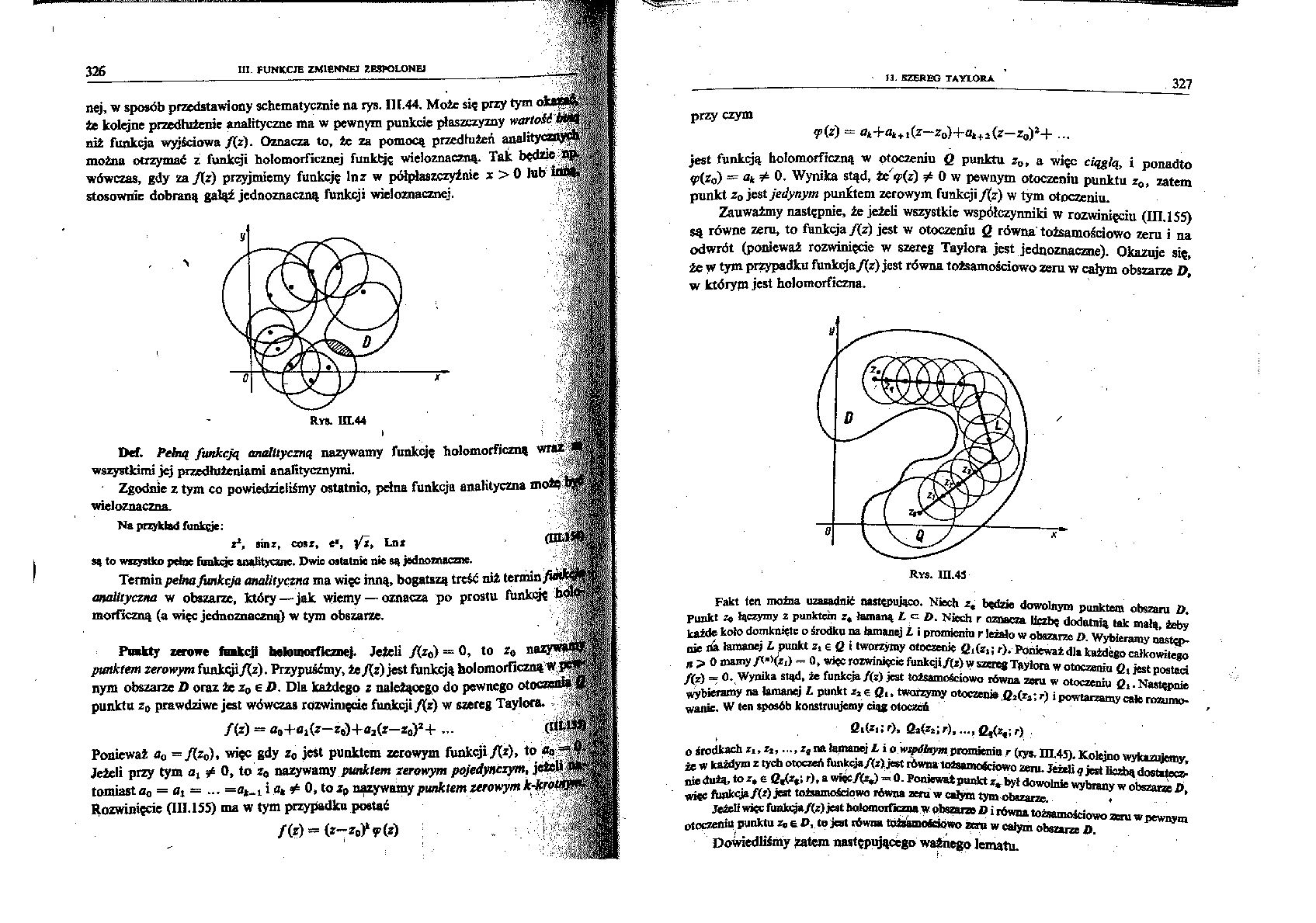
nej. w sposób przedstawiony schematycznie na rys, 1)1.44. Może się przy tym okazać, -Ą te kolejne przedłużenie analityczne ma w pewnym punkcie płaszczyzny wartoli toną A aił funkcja wyjściowa /[z). Oznacza to. te za pomocą przedłużeń an można otrzymać z funkcji holomorficznej funktję wieloznaczną. Tak wówczas, gdy za /(z) przyjmiemy funkcję In z w półplaszczyinie x >i stosownie dobraną gałąź jednoznaczną funkcji wieloznacznej.

I. FUNKCJE ZMIENNEJ ZESPOLONE)

Def. Pełna funkcją analityczną nazywamy funkcję holomorficzną wraz ■' wszystkimi jej przedłużeniami analitycznymi.    '

Zgodnie z tym co powiedzieliśmy ostatnio, pełna funkcja analityczna może b wieloznaczna.

Na przykład funkcje.

r*. siar. co»r. e*. }ft, Ln<    (IlLf^OT

są to wnystko pełne funkcje anahtycane. Dwie oetalnie me tą jednoznacaw.

Termin pełna funkcja analityczna ma więc mną. bogatszą treść niż tero analityczna w obszarze, który — jak wiemy — oznacza po prostu funkcję I morficzną (a więc jednoznaczną) w tym obszarze.

Puakty zerowe funkcji beknnorflcmej. Jeżeli /t*₀) — 0, to r₀

pwtktem zerowym funk^i/fc). Przypuśćmy, że/fc) jest funkcją holomorficzną wp _ nym obszarze Doraz te i_acD Dla każdego z należącego do pewnego otoczenia Q punktu r₀ prawdziwe jest wówczas rozwinięcie funkcji/);*) w szereg Taylora.

/W “ «a+«»(*—*ą)+«a(r—*#)*+ ...    (tlili®'!

Ponieważ 0q = ffa,), więc gdy z_c jest punktem zerowym funkcji/(z), to Oo =

Rozwinięcie (111.155) tt

Jeżeli przy tym o, * 0, to z_Q nazywamy punkiem zerowym pojedynczym, jeżeli Hf ^Ę i omast ao = 0|e* - • = o»_ > i a. + 0, to z₀ nazywamy punkiem zerowym k-kroutymiĘ^ -a w tym przypadku postać /(*) = (»-*,)>*(*)

przy czym

«*(*) “ ‘»t+a»_t,(r-jro)+a_łłl(z-Zo)^ł+ ... jest funkcją holomorficzną w otoczeniu Q punktu z_a, a więc ciągłą, i ponadto V>(z₀) = a* *■ 0. Wynika stąd, ie<p(ź) )*0w pewnym otoczeniu punktu z₀, zatem punkt z o jest jedynym punktem zerowym funkcji f(z) w tym otoczeniu.

Zauważmy następnie, że jeżeli wszystkie współczynniki w rozwinięciu (III. 155) są równe zeru, to funkcja /(z) jest w otoczeniu Q równa tożsamości owo zeru i na odwrót (ponieważ rozwinięcie w szereg Taylora jest jednoznaczne). Okazuje się, te w tym przypadku funkcja/(z) jest równa tożsamościowe zeru w całym obszarze D, w którym jest holomorficzna.

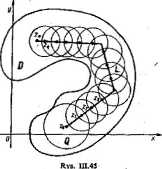
Fakt ten można uzasadnij następująco. Niech z, będzie dowolnym punktem obszaru D. Punkt z« łączymy z punktem r, łamaną I. = £>. Niech r oznacza liczbę dodatnią tak małą, żeby każde koło domknięte o środku na łamanej Z i promieniu r leżało w obszarze D. Wybieramy następnie na łamanej L punkt z, g O i tworzymy otoczenie Gifer! ')■ Ponieważ dla każdego całkowitego h > 0 mamy /i’>(zi) = 0, więc rozwinięcie funkcji /(z) w szereg Taylora w otoczeniu Ci jest postaci /(*} «= 0. Wynika stąd, że funkcja /(s) jest tożsamościowo równa zeru w otoczeniu Ci. Następnie wybieramy na łamanej L punkt zje Ci. tworzymy otoczenie Ci(z_a;r) i powtarzamy cale rozumowanie. W ten sposób konstruujemy ciąg otoczeń

Oi(*iJ r), Cn(ł>; r),C,(z_f j r)

o środkach .... z, na łamanej L i o wipdbiym promieniu r (rys. UL45). Kolejno wykazujemy, że w każdym z tych otoczeń ftmkęja/(x) jeat równa tożsamościowo zeru- Jeżeli q jest liczbą dostatecznie dużą, tor, 6 QJ£_t; r), a więc /(x^ = 0. Ponieważ punkt z, był dowolnie wybrany w obszarze D, więc funkcja/(r) jest tożsamołdowo równa zeru w całym tym obszarze.    •

Jeżeli więc Tuntoga/Cz) jest holomorficzna w obszarze D i równa tożsamościowo zeru w pewnym otoczeniu punktu z, e O, to jcal równa tożsamościowo zeru w całym obszarze D.

Dowiedliśmy zatem następującego ważnego lematu.