10691 skanuj0144 (10)

268 B. Cieślar

Pierwiastki równania wiekowego: a³ — Si a² + S2 <j - S3 = 0,

będące wartościami naprężeń głównych, obliczamy ze wzoru:

°^{k =}P ⁺ 3°_H^C0S

gdzie: k= 1,2,3;

^p=ł^s,;

®., = I(S-)^j-3S₂1^,c;

(p - kąt w radianach (lub w stopniach, jeżeli w miejsce n podstawimy 180°). Kierunki naprężeń głównych określamy przez cosinusy kierunkowe, wyznaczane z układu czterech równań (por. wzór I-5 w rozdz. I.3.4):

(o| - 85) nj = 0, ⁿj nj = 1,

gdzie:

i,j = 1,2,3,

c - naprężenie główne, którego kierunek wyznaczamy, nj - cosinusy kierunkowe naprężenia głównego o,

5y - delta Kroneckera, przy czym:

8jj" 1, jeżeli i=j, 8jj = 0, jeżeli i *\.

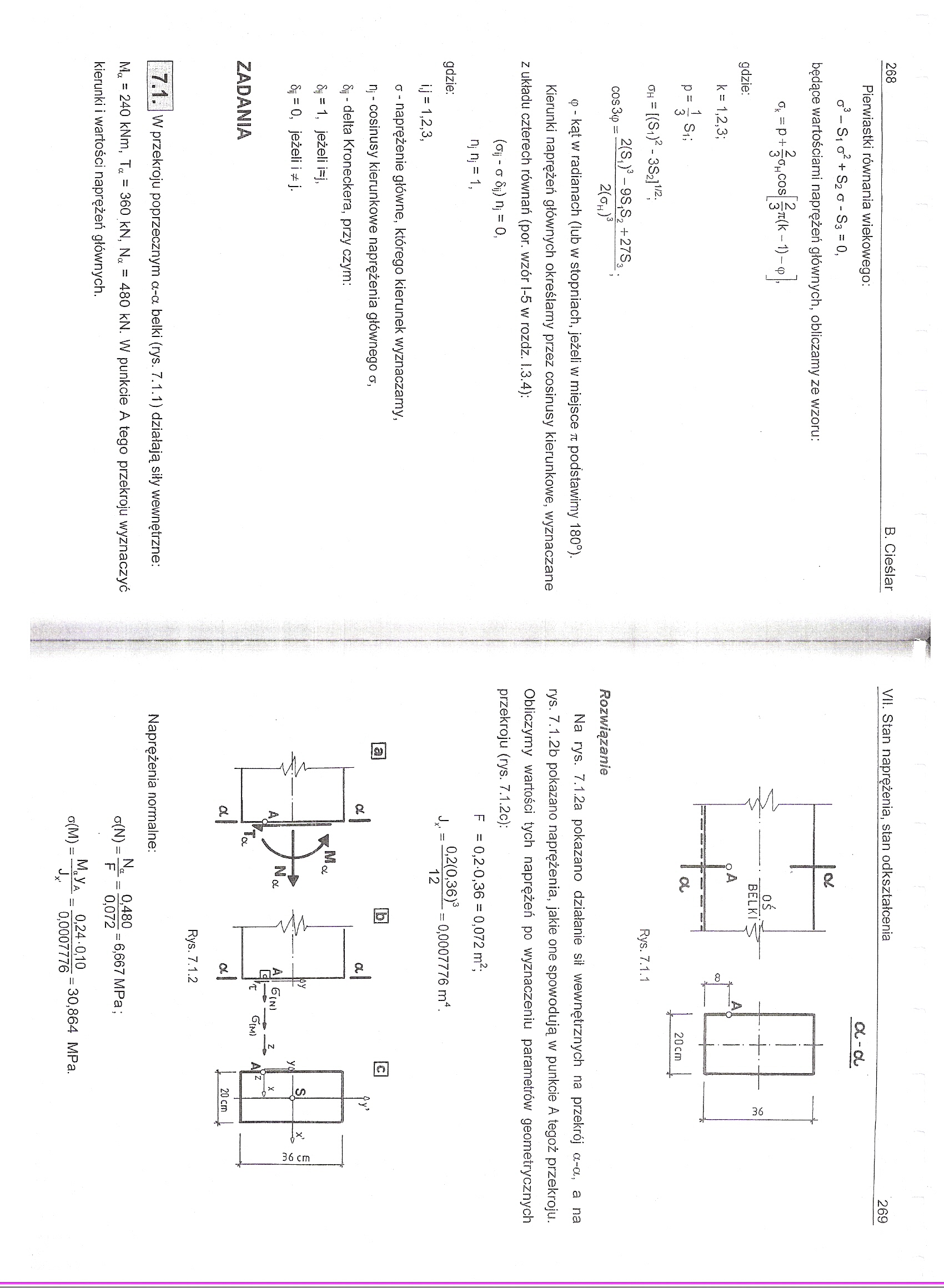
W przekroju poprzecznym a-a belki (rys. 7.1.1) działają siły wewnętrzne:

M_a = 240 kNm, T_a = 360 kN, N_a = 480 kN. W punkcie A tego przekroju wyznaczyć kierunki i wartości naprężeń głównych.

oc-oo

Rozwiązanie

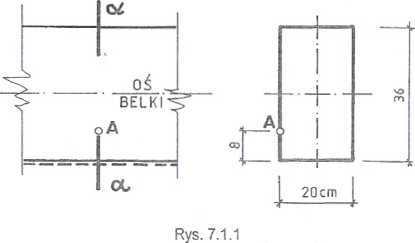
Na rys. 7.1.2a pokazano działanie sił wewnętrznych na przekrój a-a, a na rys. 7.1.2b pokazano naprężenia, jakie one spowodują w punkcie A tegoż przekroju. Obliczymy wartości tych naprężeń po wyznaczeniu parametrów geometrycznych przekroju (rys. 7.1.2c):

| = 0,20,36 = 0,072 m²;

j_x. = 0.2(036)³ _{= 0}ooo7776 m⁴.

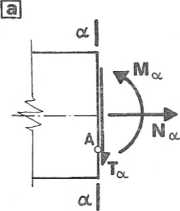
Rys. 7.1.2

Naprężenia normalne:

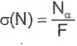
0,480

0,072

a(M) =

= 6,667 M Pa;

M_ay_A _ 0,24-0,10 J_x, 0,0007776

= 30,864

MPa.