16127 przyklad1z2

T lat

Aby wyznaczyć wartość współczynnika o skorzystamy * zależ-ności (23«)

o « 1 - 0,4 ^ - 1 - 0,4 • ^ « 0,9.

Wartość spływu Jednostkowego q dobieramy z tabeli 16. Dla terenu pagórkowatego i zlewni o długości 8,5 km odczytano:

q'= 2,8.

Szukany przepływ wielkiej wody wynosi:

Q » 18 . 2,8 . 0,9 * 45,4 m³/s.

10,8. Obli cwanie maksymalnych przepływów o określonym prawdopodobieństwie pojawiania sie na ppd8tawift--ahB9iyag.1l kYdronetrygamrcli 10.8.1. Metoda CUGW

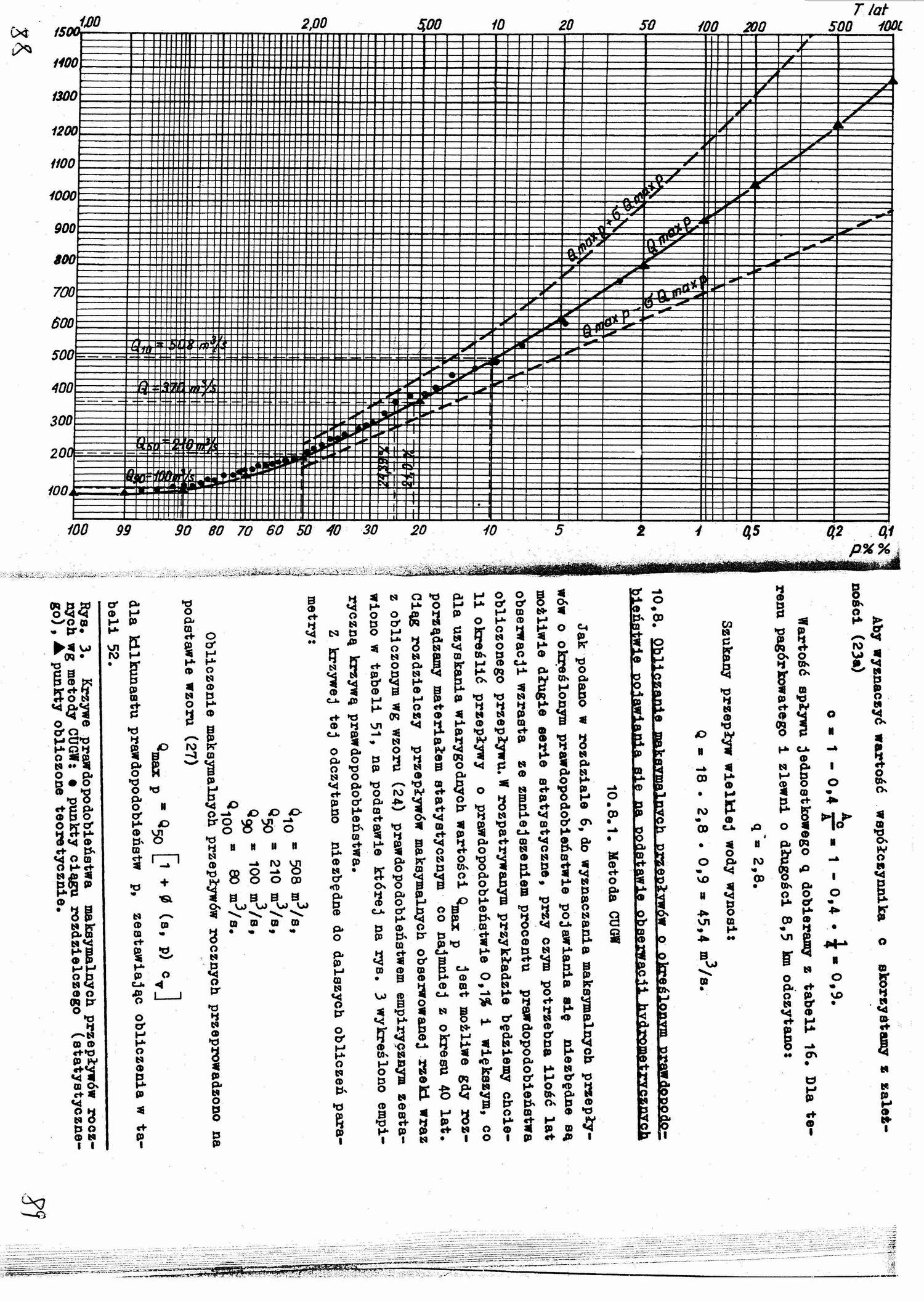
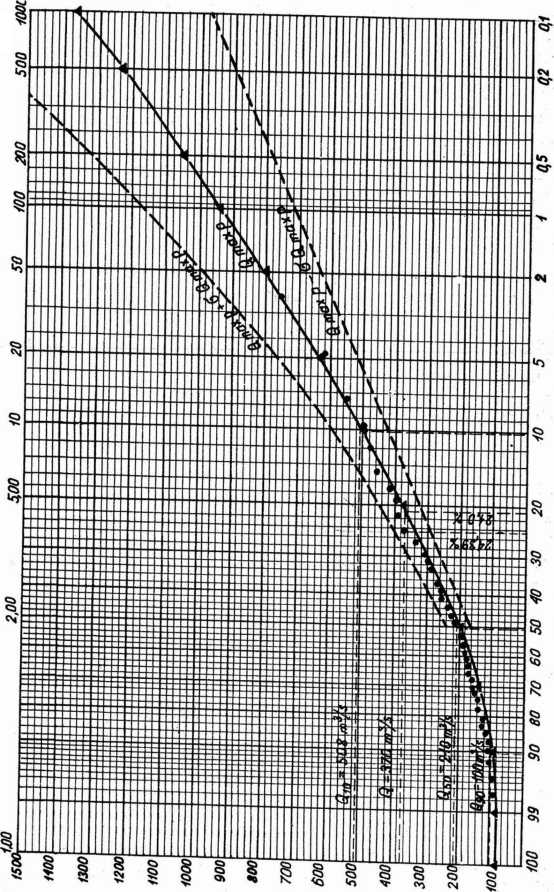
Jak podano w rozdziale 6, do wyznaczania maksymalnych przepływów o określonym prawdopodobieństwie pojawiania się niezbędne są możliwie długie serie statystyczne, przy czym potrzebna ilość lat obserwacji wzrasta ze zmniejszeniem procentu prawdopodobieństwa obliczonego przepływu.W rozpatrywanym przykładzie będziemy chcieli określić przepływy o prawdopodobieństwie 0,1% i większym, co dla uzyskania wiarygodnych wartości Q_{max p} Jest możliwe gdy rozporządzamy materiałem statystycznym co najmniej z okresu 40 lat. Ciąg rozdzielczy przepływów maksymalnych obserwowanej rzeki wraz z obliczonym wg wzoru (24) prawdopodobieństwem empiryęznym zestawiono w tabeli 51, na podstawie której na rys. 3 wykreślono empiryczną krzywą prawdopodobieństwa.

Z krzywej tej odczytano niezbędne do dalszych obliczeń parametry:

Q₁₀ - 508 m³/s,

0^ - 210 m³/s,

» 100 m³/s,

^100 " ⁸⁰ m^^s*

Obliczenie maksymalnych przepływów rocznych przeprowadzono na podstawie wzoru (27)

<W p * ^q50 [^{1 +} *^(s- »> ^ct] dla kilkunastu prawdopodobieństw p, zestawiając obliczenia w ta-beli 52._

Rys. 3. Krzywe prawdopodobieństwa maksymalnych przepływów rocznych wg metody CUGW: e punkty ciągu rozdzielczego (statystycznego) ,▲ punkty obliczone teoretycznie.

In;

p|jj