18372 Zdj�cia 0094

Oł * /’) ) * C”f ^VPj

’ w /

1

, ^,'^AVP) I ^y\(X v 1

^t). 9. u/

Ąj ’ każenie

>T ^{( P A} q )    . ^{1 Jc}" J^noważno semantycznie wymieniu:

' P A —n \ '    V * n w r.

JN*r

P) - F

P=>

)

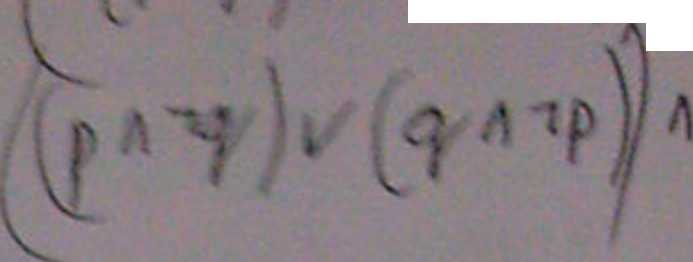
^C) (p

O) ^p AD. jo p_o^.

| ^ jc >t tautologią * ^,slrujc zastosowanie rachunku sekwentów dla spraw d.em.⁵-- »•-> fomu.hi i^a

2)

^{3) !Ł}^^ai3La)

u_->. a

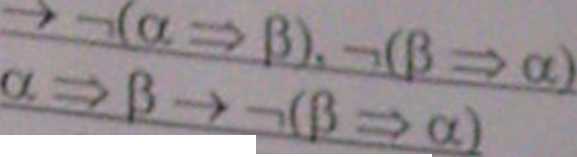
4)

v ^    a,

Zakładając /o njj , •    _____t

Xl nr 2    * ^{I /C< n}* ^vv^^zc^-i^cst poprawny, określ czy poprawnie wprowadzono w \

B)    nr    3

Q    nr    4

^D)    nr    5

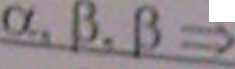
_n„_nj * . ’ ^{a ada}jqc, że x, y, / są zmiennymi indywiduowymi, p, q, r - symboUm.; prod> a;Ow • y. c>re są formułami rachunku kwantyfikatorów:

• ) /x /y • p(x, z) <=> xe {y : y^z}

Vx • —i(x o x)) => By • ->(y o y))

Vx Jy • p(x) => (3z • q(x,y,z) a (—«r(y) <=> r(y)))

^D) Vx(3x • (p(x) a q(x)))

_# • •

/Al). 12. Zakładając, żc l¹, Q są predykatami, x, y - zmiennymi indywiduowymi wskaż, n.^.w P^oruz szych formuł rachunku kwantyfikatorów są tautologiami:

Vx • Vy • P(x,y) => 3x • Vy • P(x,y)

B)    (-iVx • Vy • P(x,y) v 3x • Vy • P(x,y)) (Vx • Vy • P(x,y) a Vx • By • -:\\-> '

^    Vx • (P(x) o 0(x)) => (Vx • P(x) <» Vx • Q(x))

muła nie jest spełniona

Z\l). 14. Na pewnym etapie działania algorytm oparty o rachunek sekwentów wyprowadził z formuły F następujący zbiór sekwentów - liści drzewa dowodu:

a, -fi 2) a[x ::= yj -> a 3) Vx • a -» a, -fi 4) -a -> y. -a. p

1) ->a[x ::= t]

_1;    3) Vx • a -»a, -tp 4)-~a->

^dzie t jest różne od x. Na podstawie tego zbioru:

* ^ ' można już stwierdzić, że formuła F jest tautologią rachunku kwanty fikatorów,

3) można już stwierdzić, że formuła F nie jest tautologią rachunku kwantyfikatorów.