16814 ullman179 (2)

S ,ir_;7.YK BAZ DANYCH $QL

PRZYKŁAD 5.52

Rozważmy ponownie informację lotniczą, która służyła już jako przykład w podrożdziale 4.4. Dane na temat rejsów są zawarte w następującej relacji*:

Rejsy(linia, z, do, odlot, przylot)

Dane aktualne zostały przedstawione na rys. 4.19, który powtórzono na rys. 5.21.

AA 1900-2200

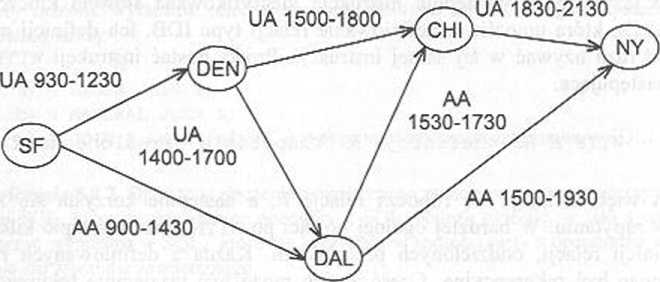
RYSUNEK 5.21

Rejsy linii lotniczych (powtórzenie rys. 4.19)

W przykładzie 4.37 szukaliśmy zbioru par miast takich, że można dostać się z pierwszego z nich do drugiego, korzystając z rejsów' uwzględnionych na rys. 5.21. W bieżącym przykładzie przedstawimy definicję relacji IDB Rejsy określonej następującymi dwiema regułami:

1. Dostępne(x, y) <— Rejsy(a, x, y, d, r)

2. Dostępne(x, y) <- Dostępne{x, z) AMD Dostępne(z, y)

2 powyższych reguł tworzymy definicję relacji Dostępne, zapisaną w SQL, której znaczenie jest takie same jak w definicji IDB. Zapytanie SQL definiujące tę relację ma postać instrukcji typu WITH. która zostaje uzupełniona stosownym zapytaniem. W przykładzie 4.37 chodziło o wszystkie możliwe połączenia, ale można formułować także zapytania o wybrane połączenia, na przykład miasta docelowe dostępne z Dctncr.

’ Słowo z oznacza miejsce odiom, a odlot czas odlotu. Odpowiednio do oznacza miejsce przylotu, a przylot - czas przylotu.

1)    WITH RF.CURSIVE Dostępne(z, do) AS

2)    (SELECT    z, do    FROM Rejsy)

3)    UNION

4)    (SELECT    R1.2,    R2.do

5)    FROM Dostępne AS Rl, Dostępne AS R2

6)    WHERE    Rl.do    R2.z)

7)    SELECT * FROM Dostępne;

RYSUNEK 5.22

Zapytanie SQL3 o pary miast połączonych

Na rysunku 5.22 przedstawiono relację Dostępne w postaci zapytani; SQL*. Wiersz 1) rozpoczyna definicję Dostępne, a jej treść jest zapisane w wierszach od 2) do 6).

Według definicji tworzona relacja powstaje w wyniku sumowania dwócł zapytań, z których każde odpowiada jednej z reguł opisujących relacje Dostępne z. przy kładu 4.37. Wiersz. 2) jest odpowiednikiem pierwszej, zasadni czej reguły. Stanowi ona, że drugie i trzecie składowe każdej krotki relacj Rej sy (wartości atrybutów z i do) tworzą krotki relacji Dostępne.

Rckurcncja wzajemna

Można sprawdzić, czy dwie relacje lub dwa predykaty są wzajemnie reku-rencyjne, stosując metodę teorii grafów. Polega ona na tym, ze konstruuje się graf zależności, którego wierzchołki reprezentują relacje (lub predykaty, gdy używamy reguł Datalogu). Między wierzchołkami A i B rysujemy łuk, jeśli definicja B bezpośrednio zależy od definicji A. Gdy korzysta się z reguł Datalogu, znaczy to. żc A występuje w treści reguły, w której nagłówku jest B. W $QL z kolei A wystąpiłoby gdzieś w definicji B, zazwyczaj w klauzuli FROM, ale również w argumentach sumy, przecięcia lub różnicy.

Jeśli wierzchołki R i S są połączone cyklem, to R i S są wzajemnie re-kurencyjne. Najczęstszy przypadek polega na pętli od R do R, która oznacza. że relacja R zależy rekurencyjnie od siebie samej.

Zauważmy, że graf zależności przypomina ten graf, który' został wprowadzony w p. 4.4.4 przy definiowaniu negacji warstwowej. Jednakże tam trzeba było różnicować zależności pozytywne i negatywne, a tutaj nic trzeba lego robić.

' W standardzie SQL3 w przypadku rekurencji liniowej w klauzuli FROM zapytania defi niująccgo relacje jest dopuszczalne tylko jedno wystąpienie relacji rekurcncyincj. Ten postula może być zrealizowany w DBMS albo nic. W wierszu 5) na rys. 5.22 są dwa wystąpienia rela cji rckurencyjncj Dostępno, więc jest to odstępstwo od standardu. Jednakże rozważamy te: przykład, ponieważ bardzo dobrze wiąże się on z przykładem 4.37. A w systemie komercyjnyn taka postać może być dopuszczalna, mimo że nie ma jej w standardzie.