23946 ScanImage017 (4)

14 ALGORYTMY WYSZUKIWANIA I SCALANIA

m» srb <m tsc& swa

II

1.9.    Udowodnij, żc istnieje gómc ograniczenie liczby instrukcji maszynowych wymaganych do przetwarzania m połączeń między n obiektami za pomocą programu 1.3. Załóż, że instrukcja przypisania w języku C^ł wymaga zawsze mniej niż c instrukcji maszynowych, gdzie c jest jakąś zadaną stałą.

1.10.    Oceń minimalną ilość czasu (w dniach), jaka byłaby niezbędna do tego, by algorytm szybkiego wyszukiwania (program 1.1) rozwiązał problem dla 10^v obiektów i 10*’ par wejściowych w komputerze mogącym wykonywać 10⁹ instrukcji na sekundę. Załóż, że każda iteracja wewnętrznej pętli for wymaga przynajmniej 10 instrukcji.

1.11.    Oceń maksymalną ilość czasu (w sekundach), jaka byłaby potrzebna do tego, by algorytm zrównoważonego szybkiego scalania (program 1.3) rozwiązał problem połączeniowy dla 10⁹ obiektów i 10* par wejściowych w komputerze mogącym wykonywać I O⁹ instrukcji na sekundę. Załóż, że każda iteracja zewnętrznej pętli while wymaga najwyżej 100 instnikcji.

1.12.    Wylicz przeciętną odległość od węzła do korzenia przy najgorszym układzie połączeń między węzłami w drzewie o T węzłach wygenerowanym przez algorytm zrównoważonego szybkiego scalania.

♦    1.13. Narysuj diagram podobny do rysunku 1.10, zaczynając od ośmiu węzłów zamiast dziewięciu.

O 1.14. Przedstaw przykładowy sekwencję par wejściowych powodującą, że algorytm zrównoważonego szybkiego scalania (program 1.3) wygeneruje ścieżkę o długości 4.

♦    1.15. Przedstaw' przykładowy sekwencję par wejściowych powodującą, że algorytm zrównoważonego szybkiego scalania z kompresją ścieżek przez połowienie (program 1.4) wygeneruje ścieżkę o długości 4.

1.16. Pokaż, jak zmodyfikować program 1.3, aby zaimplementować pełną kompresję ścieżek. Wskazówka: każdą operację scalania należy zakończyć zmianą każdego rozpatrywanego węzła w taki sposób, by wskazywał korzeń nowego drzewa.

♦    1.17. Wykonaj zadanie 1.4, ale używając algorytmu zrównoważonego szybkiego scalania z pełną kompresją ścieżek (zadanie 1.16).

f 1.18. Przedstaw przykładowy sekwencję par wejściowych powodującą, że algorytm zrównoważonego szybkiego scalania z pełną kompresją ścieżek (zadanie 1.16) wygeneruje ścieżkę o długości 4.

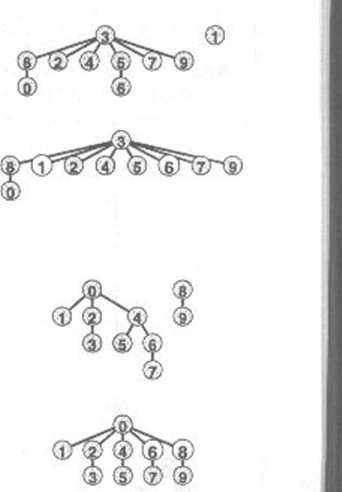
Rysunek 1.9 Kompresja ścieżek

Ścieżki w drzewach możemy skrócić jeszcze bardziej, zmieniając każdy rozpatrywany węzeł tak, by wskazywał wprost na korzeń nowego drzewa operacji scalania, jak pokazano na tych dwóch przykładach. Górny przykład przedstawia wynik odpowiadający rysunkowi 1.7. Dla krótkich ścieżek kompresja ścieżek jest bez znaczenia, jednak rozpatrując parę 1-6 zmieniamy węzły 1, 5 i 6 tak. by wskazywały na 3. uzyskując bardziej spłaszczone drzewo niż to z rysunku 1.7. Przykład u dołu przedstawia wynik korespondujący z rysunkiem 1.8. ścieżki, które nie są dłuższe niż Jeden lub dwa skoki, mogą się rozrastać w poddrzewa, ale ilekroć przez nie przechodzimy, spłaszczamy je. Tutaj przetwarzając parę 6-8, spłaszczamy drzewo zmieniając węzły 4, 6 i 8 tak. by wskazywały 0.

19 m* mm J