54487 str074 (2)

./hi,iii pięgnonoKoamic/n.i nlu ijwiii. m iii i|i > li mli n|iiin/t .-.ml,i uKlmlu Nlonoo/nngo, lo< / Jodynie wejściu nn orbity Słońcu Plorwn/ym niiinMnin, klńry osiągnął drugą prędkość kosmiczną była radziecka stacja kosmln/nn I uhm I wyttli/nlnnu nlycznla 19fS9 roku. Wyprawę w „Inno światy" gwarantuje t/.w. trzecia prędkość lumink /nn wynoB/ącu ok. 16.7 km/s. Rysunek 6.6. przedstawia dopuszczalne kształty orbit s/lm znycli nntolltów Ziemi wiążące się z określoną prędkością początkową.

Ziemia

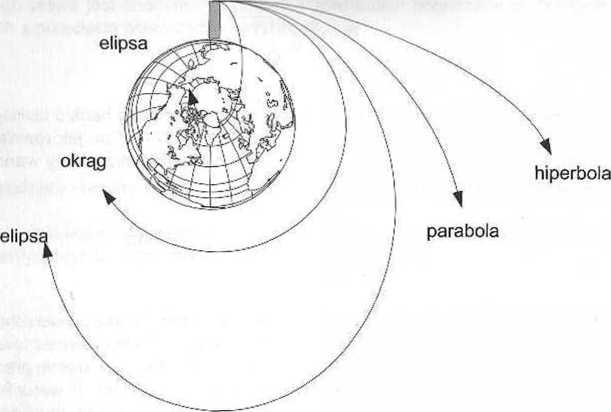
Rys. 6.6. Kształt orbity sztucznego satelity Ziemi.

Z przeprowadzonej analizy wynika ścisły związek kształtu trajektorii ruchu sztucznego '..ilullly z prędkością początkową, którą mu nadano (rys. 6.6). Związek pomiędzy prędkością początkową sztucznego satelity a kształtem jego orbity przedstawiono w poniższej tabeli.

lub. 6.2. Związek pomiędzy kształtem orbity a prędkością początkową satelity.

Kształt orbity	Prędkość początkowa satelity
Kołowa	V - V,
Eliptyczna	v,< v< v„
Paraboliczna	v= v„
Hiperboliczna	V>Vu

Z pierwszego prawa Keplera, wynika również pewna praktyczna reguła związana z sze-mkością geograficzną miejsca wystrzelenia satelity. Zgodnie z przytoczonym prawem, aby Ziemia znalazła się w jednym z ognisk figury opisującej kształt orbity, szerokość geograficzna miejsca bezpośredniego wystrzelenia satelity na orbitę może być, co najwyżej równa jej inklinacji, Oznacza to, że nie można bezpośrednio wystrzelić statku kosmicznego na orbitę u mniejszej inklinacji niż szerokość geograficzna miejsca startu. Ewentualna zmiana inklinacji orbity możliwa jest dopiero przy wykorzystaniu orbity przejściowej. Jednakże stan ten skutkuje koniecznością zużycia dodatkowej energii, co zwiększy koszty operacji. Istotnego znaczenia

1ti2

nabletii lu loknllzm.|i». /iimingo / |ę/ykn obcego, okr«>ńlmiin ><miiKKlrom" W ponlźt./o) Iriboll przedstawiono wspólizędnu gnograflczna nnjc/ęśclaj wykoi/yttlywunyoh światowych komun dromów.

Tab. 6.3. Współrzędna geograficzne najczęściej wykoi/ystywanych światowych kosmodromów

Miejsce	Państwo geograficzna	Szerokość geograficzna	Długość
Kourou	ESA*	5” N	52" W
Canaveral	USA	28° N	81° W
Vandenberg	USA	35° N	12" W
Plesetsk	Rosja	63° N	41" E
Ty u rata m	Rosja	46° N	62° E
Sriharikota	Indie	14° N	80“ E
Tanegashima	Japonia	30° N	131" 1
Shuang-Ch‘eng-Tzu	Chiny	41° N	100" I

*) ESA - Europejska Agencja Kosmiczna

Wyraźnie najkorzystniejszą lokalizację ma należący do Europejskiej Agencji Kosmlc/nn| archipelag Kourou w Gujanie Francuskiej.

6.2.3.2. Drugie prawo

Sitę grawitacji - działającą na poruszającego się po orbicie satelitę można traktować |nki > tzw. siłę centralną. Jest ona skierowana ku określonemu (centralnemu) punktowi - Zimni Rozpatrzmy ruch satelity na orbicie (rys. 6.7) pod względem jego cech geometrycznych W punkcie A na satelitę działa siła centralna (wektor AC). Gdyby na satelitę nie działało /.uInn siła to na gruncie I zasady dynamiki Newtona poruszałby się on ruchem jednostajnym prosto liniowym w kierunku punktu B zgodnie z kierunkiem wektora prędkości chwilowej w punkcie A W wyniku działania siły centralnej tor ruchu satelity ulega zakrzywieniu przesuwają; go do punktu D. Gdyby ponownie ustało działanie siły centralnej, satelita przemieściłby się do punktu E. Ponieważ prędkość liniowa satelity jest stała - stąd wynika, że AD=DE. W wyniku dzliiłnnli i siły grawitacyjnej (wektor DF) satelita poruszać się będzie po odcinku DG, będącym pr/n-kątną równoległoboku DEGF.

15: