63385 skanuj0012 (370)

24 Mathcad. Ćwiczenia

24 Mathcad. Ćwiczenia

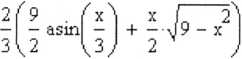
m :=

Rysunek 2.24.

Kompletna definicja funkcji użytkownika

3. Dysponując zdefiniowaną funkcją G, można obecnie zwięźle (rysunek 2.25) zażądać podania jej wartości, np. dla wartości x wynoszących 0, 0.5 i 1; nie ma przy tym konieczności trzykrotnego przepisywania złożonego wyrażenia.

Rysunek 2.25.    G(Q) = 0

Użycie zdefiniowanej

.funkcji    G(0.5) = 0.995

G(d= 1.962 ,

Imienne zakresowe

Mathcad potrafi wykonać powtarzalne obliczenia dla różnych wartości argumentów. Służy do tego specjalny typ zmiennych, noszących nazwę zmiennych zakresowych. Są one de facto ciągami arytmetycznymi. Zdefiniowane wcześniej wyrażenia obliczane są dla każdego elementu takiego ciągu. Dzięki temu zmienne zakresowe są idealnym narzędziem np. do tabelaryzacji wartości funkcji. Dostępne są dwa rodzaje definicji zmiennych zakresowych (tabela 2.4):

❖ z krokiem przyrostu o wartości 1 — do definiowania zmiennej zakresowej służy pierwsza i ostatnia wartość ciągu;

♦> z krokiem przyrostu różnym od wartości 1 — do definiowania zmiennej zakresowej służy pierwsza, druga i ostatnia wartość ciągu.

Tabela 2.6. Definiowanie zmiennych zakresowych

Opis	Sekwencja klawiszy	Przykład
Zmienna zakresowa o nazwie i definiowana jako ciąg od a do b co 1		i := a .. b
Zmienna zakresowa o nazwie i definiowana od a z drugim wyrazem b do c		i := a. b .. c

Ćwiczenie 2.7. —

Oblicz wartości funkcji sin od (f do 10° w odstępie 1°.

1. Zdefiniuj zmienną zakresową o nazwie kat o wartościach od 0 do 10 co 1 (rysunek 2.26).

kat := 0.. 10

Rysunek 2.26.

Definicja zmiennej zakresowej kat