63544 kralS

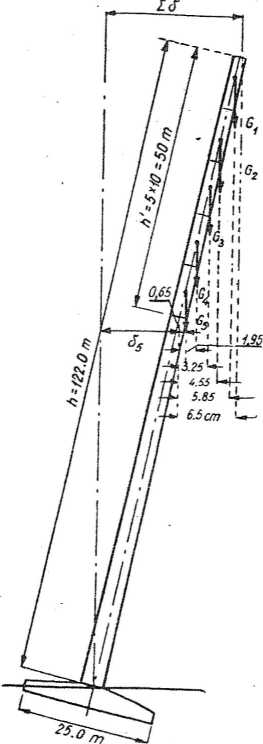
Rys. 45. Wymiary do obliczenia momentu od wychylenia trzonu komina

Następnie wyliczamy ramiona sił: Gj = 134,8 T; = 5,85 cm; G₂ = 143,1 T; x₂ = 4,55 cm; G₃ = 168,3 T; x₃ = 3,25 cm; G₄ = 189,1 T; x₄ = 1,95 cm; G₅ = 211' T; x₅ = 0,65 ćm; 5d,

przyjmując dla uproszczenia zaczepienie sił w środku wysokości członów.

ZM = 134,8 • 0,0585+143,1 • 0,0455+168,3 • 0,0325 + 189,1 • 0,0195+211, •

• 0,0065 = 7,88+6,52+5,47+3,69+1,37 = 24,93 Tm.

Wartość otrzymanego momentu w stosunku do momentu zasadniczego wynosi 24,93 -100

—j— = 2,1%, a więc jest niewielka, tym niemniej doliczamy ją do momentu zasadniczego i ostatecznie do obliczeń naprężeń przyjmujemy M_x>

= 1177,5+24,93 = 1202,5 Tm.

E6 15,8    1

Stosunek wielkości odkształcenia do wysokości komina — =-=-<

^J    h 12200    775_j

1

a więc jest prawie dwukrotnie mniejszy od dopuszczalnego.

Jeśli chodzi o dynamiczny wpływ parcia wiatru na komin, to z punktu widzenia teoretycznego jest to zagadnienie dość skomplikowane i trudno uchwytne. Norma kominowa uwzględnia wpływy dynamiczne wiatru w postaci współczynnika dynamicznego f, zależnego od wysokości komina H [m], mierzonej od poziomu jego utwierdzenia w fundamencie i od podstawowego okresu drgań własnych T [s].

Przybliżony wzór na obliczenie okresu podstawowych drgań własnych T dla kominów o jednostajnej zbieżności i zmniejszającej się grubości ściany według rys. 46:

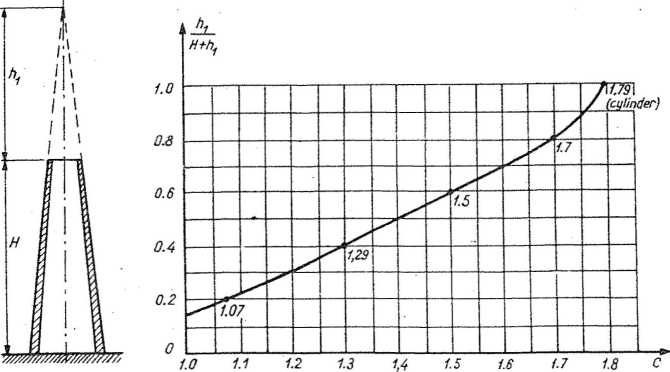
Rys. 46. Wykres współczynników C i oznaczenie H do wzoru na okres drgań własnych komina

zbieżnego

T =C-W

]/

V E-J-g

w.

105