67027 Untitled Scanned 46 (2)

PLANIMETRIA 49

PLANIMETRIA 49

4 m

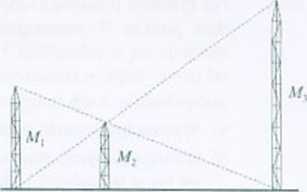
333. Na rysunku przedstawiono wzajemne położenie trzech masztów antenowych znajdujących się na terenie Institute of Telecomuni-cations w Melbourne. Maszty ustawione są w linii prostej, a wysokości skrajnych masztów M\ i Mi są równe: 140 m i 260 m (patrz rysunek).

a)    w Oblicz wysokość najniższego masztu.

b)    Oblicz odległości między masztami M₍ i M_: oraz M. i M. wiedząc dodatkowo, że maszty A/, i A/-, ustawione są w odległości 300 ni.

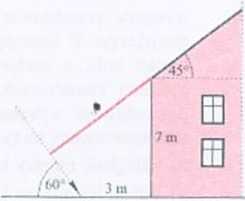
334. Na rysunku pokazany jest fragment domku jednorodzinnego. Pewnego słonecznego dnia w południe promienie słoneczne padały pod kątem 60° do poziomu. Oblicz długość okapu dachu (części dachu wystającej poza ścianę budynku) wiedząc, że szerokość zacienionego pasa ziemi wzdłuż ściany budynku była równa 3 m. Pozostałe dane zamieszczono na rysunku.

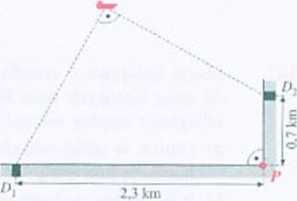
335. Statek, który wpłynął do portu kieruje się do punktu przeładunkowego H. Na rysunku przedstawiono położenie statku względem nabrzeża portowego w momencie, gdy znajdował się w równych odległościach od dźwigów portowych D\ i /X

a)    Oblicz odległość statku od dźwigów portowych.

b)    Znajdź odległość statku od punktu przeładunkowego Wyniki podaj w kilometrach.

336. Lampa zawieszona na wysokości 4 m oświetla powierzchnię w kształcie koła.

a)    Postanowiono zawiesić lampę o 2 m wyżej. Oblicz, o ile procent wzrosła powierzchnia oświetlona przez lampę.

b)    Oblicz, na jakiej wysokości należałoby zawiesie tę lampę, aby oświetlała dwukrotnie większą powierzchnię.

337. Pewnego dnia w południe cień masztu miał długość 17,6 m. Po kilku godzinach, gdy promienie słoneczne tworzyły z powierzchnią ziemi kąt dwa razy mniejszy niż w południe, cień masztu miał długość 45 m.

a)    Oblicz wysokość masztu.

b)    Oblicz pod jakim kątem do powierzchni ziemi padały promienie słoneczne w południe. Wynik zaokrą-gli j do pełnych stopni.

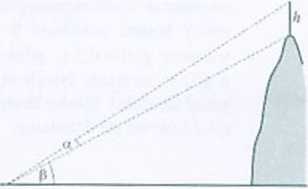
338.    7 pewnego punktu w terenie, dokonano pomiaru kąta a pod

jakim widać maszt telewizyjny wybudowany na szczycie góry oraz pomiaru kąta (i pod jakim widać górę (rysunek obok).

Wysokość masztu jest znana i wynosi h.

a)    Znajdź zależność między wysokością H góry. a wielkościami a. (i i h.

b)    Przyrząd pomiarowy pokazał wartości: tg« = 0.05, tg/?= 0,45. Wiedząc, że maszt ma wysokość 20 m, oblicz wysokość góry. Wynik podaj w metrach po zaokrągleniu do jedności.