70245 skanuj0005 (384)

2. Ramy. Przykłady rozwiązań analitycznych

2.1. Rama prosta jednotarczowa

Przykład 9. Ramę rozwiązać analitycznie. Sporządzić wykresy sił przekrojowych.

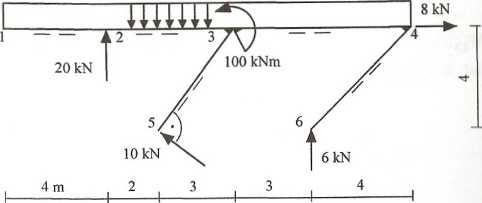
Schemat statyczny

2 kN/m

Z analizy schematu statycznego wynika, że jest to ustrój jednotarczowy połączony z fundamentem trzema więziami nieprzecinającymi się w jednym punkcie. Zachowany jest zatem warunek ilościowy i jakościowy geometrycznej niezmienności, schemat jest statycznie wyznaczalny. Z geometrii podparcia 4    3    4

wynika, że tg a * - stąd cos a = sina = zaś składowe reakcji R wynoszą 3    .43

Ry ■ R cos a = -R, R_x = R sina = - R, R_y = - R_x. Dla układu jednotar-

czowego zawsze można wybrać taki wariant równowagi, aby niewiadome reakcje wyznaczyć niezależnie. W tym zadaniu w sposób niezależny wyznaczamy jedynie reakcję R wykorzystując warunek rzutów.

XXmO, +8 — R_x = 0, R_x=+8kN, R_y = 6 kN, R = 10 kN.

Z równowagi momentowej względem bieguna

IMi » 0,    F*8—R_y*6+8*4—100—2*16*4 = 0, F = +20 kN.

Z warunku rzutów na oś pionową Y otrzymujemy

IY = 0    V+R_y+W-2*16 = 0, W = 6 kN.

Do wyznaczenia sił przekrojowych często korzysta się ze schematu obliczeniowego, w którym występują wszystkie obciążenia zewnętrzne z już poprawnymi zwrotami (może się zdarzyć, że niektóre reakcje w wyniku obliczeń mają znak minus).

Siły przekrojowo wyznaczamy metodą statyczną rzędnych charaktorystycz-2H nych, zaczynając od prętów nachylonych (włókna uprzywilejowane pokazano na rysunku wraz z opisem charakterystycznych punktów).

Schemat obliczeniowy 2 kN/m

N53 — 0 = N35,

Pręt 5-3

r₅₃=+iokN = r₃₅,

M_s = 0,    M₃₅ = +10- 5 = +50 kNm,

Pręt 6-4

N"= -6-y/2/2-kN = N_46>

T₆₄ = +6-V2/2= +3^2 kN = N_i6,

Af₄= +6-4= +24 kN.

Siły w przedziałach pręta poziomego wyznaczamy po dokonaniu redukcji obciążeń z prętów nachylonych do osi pręta poziomego — metoda od przekroju do przekroju.

2 kN/m

		:.UU A7 s			V-*
^2t		50kNm \|*8kN		^4,	^k ^24 kNm
20 kN		6 kN		6 kN
_im_u		5 _L______	7

X|₂, x₂₃    x„

Łatwo zauważyć, że przedstawiony pręt znajduje się w równowadze. Można by kontynuować wyznaczanie rzędnych w przekrojach charakterystycznych; przedstawimy tu jednak relacje funkcyjne dla poszczególnych przedziałów wg przyjętych zmiennych goomotrycznych jak na rysunku.