72783 skrypt040 (2)

7H Laboratorium Podstaw Elektrotechniki 1

7H Laboratorium Podstaw Elektrotechniki 1

Tablica 4.2

Lp.	U	I
	V	A
1
2
3

Tablica 4.3

Metoda	I	Ul	U2
	A	V	V
a..
b.
c.

Dla wybranej wartości napięcia zasilającego U pomierzyć prąd l oraz napięcia Uj i U2 na obu elementach nieliniowych. W tablicy 4.3 zestawić wyniki dla wybranej wartości napięcia otrzymane w następujący sposób:

a.    na podstawie wykresu charakterystyki łącznej i charakterystyk poszczególnych elementów,

b.    na podstawie pomiaru,

c.    metodą przecięcia charakterystyk.

Ocenić zgodność pomiarów z charakterystykami wyznaczonymi graficznie w punkcie 4.2.1,

4.2.3. Pomiar charakterystyki połączenia równoległego dwóch elementów nieliniowych

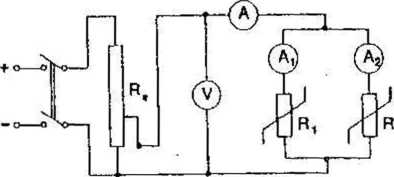
Rys.4.9. Uktad pomiarowy dla połączenia równoległego.

Połączyć obwód jak na rys.4.9 i pomierzyć charakterystykę l=Ij+l2=f(U) dla połączenia równoległego dwóch elementów nieliniowych, notując wyniki w tablicy 4.4. Na podstawie uzyskanych wyników narysować charakterystykę I-tfU),

Dla zadanej wartości prądu I należy wyznaczyć wartości prądów 11 i I2 w obydwu gałęziach. W tai)licy 4.,'i zestawić wyniki dla zadanej wartości prądu otrzymane w następujący sposób:

a.    na podstawie wykresu charakterystyki łącznej i charakterystyk poszczególnych elementów,

b.    na podstawie pomiaru,

c.    metodą przecięcia charakterystyk.

Ocenić zgodność pomiarów z charakterystykami wyznaczonymi graficznie w punkcie 4.2.1.

Tablica 4.5

Metoda	u	h	*2
	V	A	A
a.
b.
c.

Tablica 4.4

4.2.4.    Rezystancja statyczna i dynamiczna

Dla poszczególnych elementów wyznaczyć zakresy zmienności rezystancji slatyczuej i dynamicznej.

4.2.5.    Aproksymacja charakterystyk doświadczalnych

Znaleźć równanie aproksymującc charakterystyki E=f(U) elementów użytych w ćwiczeniach. Zastosować w tym celu funkcję aproksynmjącą o postaci

I = b- U<*

(4.8)

Równanie to po zlogarylmowaniu przybiera postać

logi = logb + d-logU    (4.9)

Dla kilku punktów wykreślonej z pomiarów charakterystyki l~f(U) obliczamy wartości logarytmów I oraz U i zestawiamy je w tablicy 4.6. Zależność iogI=f(logU) jest w przybliżeniu linią prostą.