77909 P3200171

270 4. Analiza skupień

Pewna doza niepewności, jaka tkwi w tych dwóch metodach, a zwłaszcza w metodzie najbliższego sąsiada, może być zredukowana dzięki metodzie średniej grupowej lub średniego połączenia (ang. average linkage, group average cluste-ring, unweighted average link) . Jest to technika przeliczania odległości, która uwalnia nas od konieczności wyboru bądź to najbliższego, bądź też najdalszego sąsiada z dwóch różnych skupień obiektów, a w szczególności uwalnia od wrażliwości na wartości ekstremalne. Podstawę metody stanowi koncepcja średniej odległości, którą jest średnia arytmetyczna odległości między wszystkimi parami obiektów należących do dwóch porównywanych grup

2

k€p

(4.97)

gdzie - odległość między /-tym obiektem należącym do skupienia i (j - 1 a k-tym obiektem należącym do nowotworzonego skupienia p = r U s(k = 1 ,...,n_p), przy czym suma rozciąga się na wszystkie n, • n_p par obiektów z dwóch skupień, przy czym n = n_r + n₍.

Do algorytmicznego przeliczania odległości między skupieniem i a skupieniem p stosuje się wzór na średnią ważoną

n.    n.

d. = ~d_ir + -^Ld_is    (4.98)

^{v n}~

p    p

gdzie: 4 i 4 - średnie odległości punktów grupy i od punktów grupy, odpowiednio r i s, które wyznaczono zgodnie z tą zasadą w poprzednim kroku, n, i n, - liczby elementów w grupach r i s, przy czym n_p- n_r+ n_s.

Łączone są te dwa skupienia, dla których średnia odległość jest najmniejsza.

W przeciwieństwie do dwóch pierwszych metod, metoda średniej grupowej nie zależy już w tak dużym stopniu od wartości skrajnych. Wykazuje ona tendencję do łączenia skupień o małych i raczej równych wariancjach (Hair i in. 1995). Ujemną stroną metody średniej grupowej jest to, że w przypadku metrycznego pomiaru odległości, tworzone skupienia zależą od użytego typu funkcji odległości między jednostkami (zob. Gnanadesikan, 1997). Twierdzi się, iż metoda średniej grupowej daje konfigurację połączeń podobną jak metoda najdalszego sąsiada, lecz inny sposób przeliczania odległości powoduje, że połączenia następują na innym poziomie odległości, ostatnie - zwykle na niższym. Wydaje się, że właściwszym będzie stwierdzenie, iż daje ona konfigurację pośrednią między metodami najbliższego i najdalszego sąsiada. Odległości między skupieniami są bardziej

ⁿ Została ona za proponowana przez R.R. Sokala i C.D. Michenera w 1958 roku wyważone - większe niż w metodzie najbliższego sąsiada i mniejsze niż w metodzie najdalszego sąsiada⁸³.

Słabą stroną metody średniej grupowej jest to, że skupienia nie mają zdefi niowanych centrów.

Przykład 4.5. (grupowanie hierarchiczne - metoda średniej grupowej)

Metoda średniej grupowej zastosowana do macierzy odległości D¹* z przykładu 4.3 dała kolejny, trzeci wynik grupowania Zbiera on własności dwóch wcześniejszych ugrupowań. Wydaje się, że w odniesieniu do hierarchii grupowania dendrogram na wykresie 4.10 jest w jednej części (lewej) podobny do dendrogramu w metodzie najdalszego sąsiada, w drugie) zaś części (prawej; bar dziej przypomina dendrogram w metodzie najbliższego sąsiada |est on dosta tecznie przejrzysty i wskazuje na istnienie następujących skupień (5, 6, 4... (2, 7. 1) oraz jednostki izolowanej (3).

Można przy okazji sprawdzić empirycznie poprawność wzoru (4 97) Weźmy przykładowo dwa skupienia: (2, 7, 1) oraz jednoelementowe skupienie (3; Suma odległości wszystkich par obiektów należących do odrębnych skupień wynosi d -f d₃ 7 + <f₃ j = 8,54 + 4,91 + 3,50 = 16,95, a zatem średnia odległość jest rów na 16,95/(3* 1) = 5,65, czyli tak jak zaznaczono na dendrogramie zob rysunek

4.10).

Poziomy

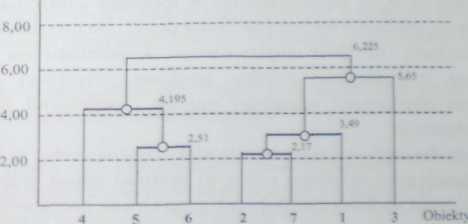
Rysunek 4.10. Dendrogram (metoda średniej grupowej

W Jest też inna metoda oparta na średnim połączeniu metoda średniej ważonej (ang. weighted avt rugę link), która godzi metodę najbliższego i najdalszego sąsiada Ma ona prosty algorytm przeliczający odległości: d    + d' ) 2. który nie uwzględnia liczności łączonych grup. czyli nie przy

pisuje każdemu obiektowi w skupisku tej samej wagi. Zaproponował ją L.L. McQuitty w roku 1966.