P1100199

c

ł

y

* i i

CóMnamh ty pidshmmli j i, UlHlMi} «

Odmłmki * . cdrititiu I j

SwMtwit di 2 4 j mnmfo 2 J y

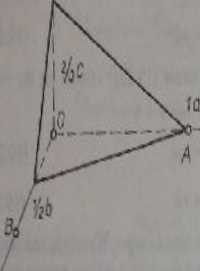
Rji 19.23. Płaszczyzna klóra odcina ki osiach odcinki ltf, 10. lik pny czy® q_a

OA - A, OC - jednostkowy oddaek c    *

* pr-uw) opici rysunku pokanno sposób postępo’.vania przy wyprowadzaniu «kiWsi_

Millera płaszczyzny

W kystalogmlii orientacje płaszczyzn wyraża się za pośrednictwem wsłaj. ników Millera, Są to liczby względem siebie pierwsze, całkowite (dodatnie, ujemne i zero), które się wyprowadza zgodnie ze sposobem przedstawionym na rys. jpy Jeżeli jedną z ekwiwalentnych płaszczyzn przechodzi przez punkty ||i| które leżą na osiach x,y, z i odcina na nich odcinki k b\2,2c/3, wtedy wskaźniki Millera takiej płaszczymy są adwrotnośdani wartości odcinków (liczby całkowite),

ł

Z

i t

i

i (200J

(m)

i

i

(102)

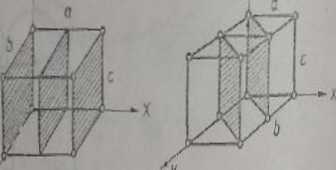
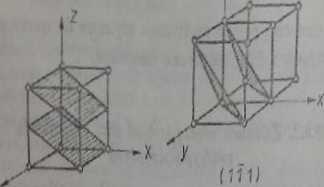
R/ł. 19.24. Niektóre plaamymy sieci bysufeiuj z ich wjbinibmi Mflkrł

Które na osiach odcina rozważana płaszczyzna (w jednostkach podstawowych wektorów «. b. c), n więc mają wartości 2.4, 3. Równoległość płaszczyzny do którejś oti oznacza, że płaszczyzna przecina oś w nieskończoności, co po analogicznym opracowaniu, jak przedstawiono na rys. 19.23, prowadzi do zerowej wartości wskaźnika. Jeżeli Jakaś płaszczyzna ma tuką orientacją, że dzieli odcinek na ujemnej części osi. wskaźnik ma wartość ujemną.

Niektóre przykłady płaszczyzn sieci z ich Wskaźnikami Millera przedstawiono nn rys. 19.24. Jeżeli wskaźniki Millera są w nawiasach okrągłych, oznacza to układ płaszczyzn ekwiwalentnych.

Odległość między płaszczy/nowa d jest funkcją stałych sieci i zależy również, od orientacji płaszczyzn, a więc od wskaźników Millera

d =*f (a, b_t c, cc, fi, y, Ji, fc, ł)    (19.23)

Dla układu współrzędnych prostopadłych ta zależność funkcyjna jest prosta. Dla najbardziej powszechnego układu trójslcoftnego funkcją jest dość złożona. Niektóre prostsze postaci równania (19.23) dla układów współrzędnych prostopadłych można wyprowadzić zgodnie z rys. 19.25 i można je znaleźć w tabl. 19.2.

Tablica 19.2. Zależności dla odległości międżyplaszcżyzńósrycti

Struktura regularna ja - g*	Struktura tetragonalna ^ , _ a*
A* + A*f/*	*! + *»+/» .sL
Struktura heksagonalna	Struktura ortorombowa
i* -	rf. _ 1
— (A*+ A*+AA)+/* ~	k* k* P
3 e*	<p 6* c*

Struktura trygonalna

_    q(H-2cos^aq—3 cos^ł«) _

’    2 (AA t- A/-t- kQ (ęae?a -cosa)

Struktura jednotkośna

fi* m

I

d*nin*fi

P . 2A/cosfl . A* c^asin*jś oMn^>J b*

Struktura trójakośna

d* -

— COS/ COS/?		1 Aco5/ł		1 cosy —
1 a		a
Aft.	. *	k	/	. A
- v 1 cau a ó	ó	CO«7~COM O	— c	co* 1
U co- 1		co*/? ~ 1		cosJ cosj --
1 c		c

1 cos/cosjf ;cosy I tfOM ęoij cosa 1