skanuj0012

ZESTAW 3 - POZIOM PODSTAWOWY

Zadanie 1. (3 pkt)

W klasie sportowej pewnego liceum jest 12 dziewcząt i 18 chłopców. Na uroczystość wręczenia nagrody kuratora oświaty za uzyskanie bardzo dobrych wyników sportowych należy losowo wybrać trzyosobową delegację. Jakie jest prawdopodobieństwo, że znajdzie się w niej dokładnie jeden chłopiec?

Zadaniu 2. (3 pkt)

W tabeli podano wysokość miesięcznego wynagrodzenia pracowników pewnej spółki.

Miesięczne wynagrodzenie w zł	950	1200	1500	2000	2500	4000	6000
Liczba pracowników otrzymujących wynagrodzenie w podanej wysokości	20	17	12	8	3	3	1

a)    Jakie jest średnic miesięczne wynagrodzenie w tej spółce?

b)    Ilu pracowników tej spółki zarabia miesięcznie poniżej średniego wynagrodzenia mie sięczncgo?

Zadanie 3. (4 pkt)

W basenie znajduje się 2400 m' wody. Przy otwartym zaworze w ciągu minuty można / basenu spuścić 8 m ’ wody.

a)    Wyraź objętość Vwody pozostającej w basenie jako funkcję czasu /. Podaj dziedzinę funkcji.

b)    Po jakim czasie pozostanie w basenie S(K) m' wody?

c)    Po ilu godzinach basen będzie pusty?

U-*1 + I2v-3| -314-.VI , |.3r-4|

Zadanie 4. (4 pkt)

Uzasadnij, że dla x < I prawdziwa jest równość:

Zadanie 5. (5 pkt)

Pewna parabola o wierzchołku W = (1,3) przecina oś OY w punkcie A = (0, I).

a)    Wyznacz wzór funkcji kwadratowej, której wykresem jest ta parabola.

b)    Oblicz miejsca zerowe funkcji kwadratowej.

Zadanie 6. (4 pkt)

Koło ma średnicę długości 12 cm.

a)    O ile centymetrów' zwiększy się obwód kola, jeśli jego średnicę zwiększymy o 4 cm?

b)    O ile procent zwiększy się pole kola, jeżeli promień zwiększymy o 3 cm?

Zadanie 7. (5 pkt)

Wiedząc, że sin a - 0,6 i « 6 rrj:

a)    zbuduj kąt a,

b)    oblicz wartości pozostałych funkcji trygonometrycznych kąta a.

Zadanie 8. (4 pkt)

Punkty A = (0,-1),/? = (7, -2), C = (6,5), D - (-1,6) są wierzchołkami czworokąta MU I). a) Wyznacz równania prostych, w których zawierają się przekątne c/w.u.4 iu h) l J/asadnij, żc przekątne czworokąta są prostopadle

Zadanie 9. (5 pkt)

Na rysunku przedstawiono część wykresu nieskończonego ciągu geometrycznego («„). Wyznacz wzór na ogólny wyraz tego ciągu.

6 .........•

5

4 .........V

3 2 I

TĄ I 2 3 4 5

Zadanie 10. (7 pkt)

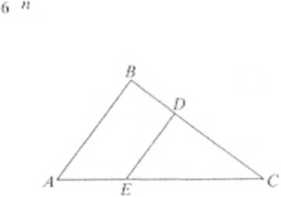
Długości boków trójkąta są równe: \AH\ = 9 cm,

|/iC| = 12 cm, \AC\ = 15 cm. Odcinek DE jest równoległy do boku Ali. Obwód trójkąta CDE jest równy obwodowi trapezu A li DPI. Oblicz długość odcinka DE.

Zadanie 11. (6 pkt)

t )bjętość prostopadłościanu, którego wysokość ma długość 10 cm. równa się 480 cm' Stosunek długości krawędzi podstawy wynosi 3 : 4. Wyznacz miarę kąta nachylenia przekątnej prostopu • Ilościami do płaszczyzny podstawy. Sporządź rysunek prostopadłościanu i zaznacz szukany kąt

ZESTAW 3 - POZIOM ROZSZERZONY

/udanie 12. (4 pkt)

I )wóch strzelców, spośród których pierwszy na 100 strzałów trafia w tarczę średnio 60 razy. di ngi 70 razy. oddaje równocześnie |X) jednym strzale do tarczy. Oblicz prawdopodobieństwo trafienia w tarczę przez:

.i) obu strzelców,

b) co najmniej jednego ze strzelców.

/.idanie 13. (3 pkt)

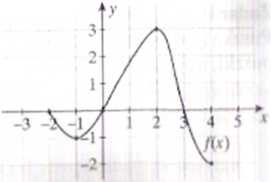
Na rysunku przedstawiono wykres pewnej funkcji f.

.0 Narysuj wykres funkcji pokreślonej wzorem g(x) = /(-.v). b) Zapisz przedziały, w których funkcja p jest malejąca.