244 (10)

natomiast /‘"jest taką, odczytywaną z tablic (tab.V), wartością zmiennej o rozkładzie F-Snedecora, że (na ogół przyjmuje się y= 0.95). Wielkości P_Xj, Py_t, Px,Y_t elementami bloku

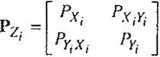
(^PY,X, ~ ^PXjYj )

wyjętego, dla każdego z punktów Z_jt z macierzy

%

^PZ,.Z₂

A PA =

Pz₂.z, ^pz*

p,

L^pz_e._Z| ^pz,.z₂

Po

z.

5.1.5. Podstawowe zastosowania

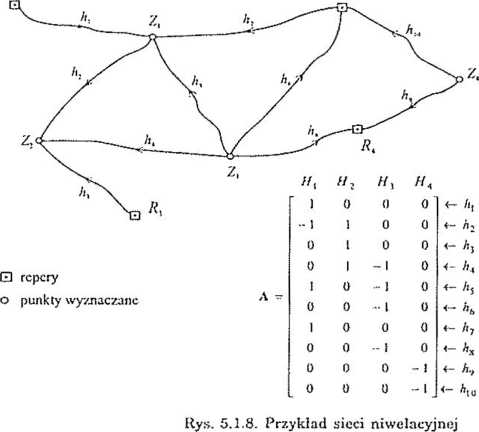
Sieci niwelacyjne w układzie (//)

Takie sieci geodezyjne znajdują zastosowanie w wielu technicznych problemach geodezji, a przy tym „generują” najprostsze, liniowe układy równań obserwacyjnych. W sieciach niwelacyjnych pomiarowi podlegają przewyższenia hjj między punktami Z₍, Zj

H A

Rys. 5.1.7. Przewyższenie między dwoma punktami

Przyjmując jako parametry wysokości H_j} H: tych punktów, odpowiednie równanie obserwacyjne można przedstawić w postaci

Ponieważ prawdziwa wartość przewyższenia h- jest sumą wyniku pomiaru h-j* i nieznanej poprawki Vy, więc

Uzyskane równanie poprawki jest liniowe względem nieznanych parametrów H_t, //.. Nie ma więc potrzeby rozwijania go w szereg Taylora w otoczeniu jakichś przybliżonych wartości tych parametrów (tutaj - przybliżonych wysokości punktów). W takim przypadku wektor niewiadomych X w modelu funkcjonalnym V - AX + L tworzą „całe” wysokości punktów. Elementy macierzy A przyjmują którąś z wartości: -1, 0, 1, natomiast wyrazami wolnymi są ujemne wartości wyników pomiaru przewyższeń, tzn. l_t} =~-h‘j^h (w niektórych przypadkach redukowane o znane wysokości reperów, zob. przykład 5.1.1).

(5.1.48)

L--

n 10

r~ 4

/= 6

W?

-//₃°

-*?

tli

-tti

-Ha

K

K

-A?

-hl

,.v>

f oA

W celu ułatwienia obliczeń można jednak także przyjąć, że są znane pewne, na przykład ustalone na podstawie wyników pomiaru przewyższeń, przybliżone wysokości //_t°, Hj punktów Z_jt Zj (podkreślmy: ze względu na liniowy charakter funkcji /^(//y, Hj), przybliżenia te mogą być w zasadzie dowolne). Wówczas

H,=H?+d_H.

245