292 (9)

- kątów

CX^ — ^J3 20 “ '^13,21 ~ 42 57 50 /3 — Aoq t ] — Moo j 3 "r 360 = 56 j3 54

7° = "bo.22 - ^20.21 = 62*5l'46' r = '^22 21 ^— Aoo ->o “ 45 55 40

Ponadto obliczamy (na podstawie znanych współrzędnych punktów stałych): d|₃.20 = /(*20 ~*,₃)² +(y₂₀~ ł^)² = 1979.23 (m)

^20.22 ~ X22 ~ X oq)~ + (^22 “ ^20 )~ ~ 1802.31 (m)

{

A, 3.20 = 180" +

arctą ■

^20 ~ ^13 X 20 - X • 3

p = l63°38^/33'

A-,g — 180 -f-

(    V

1 no

arctsr •~—

--*L )p = |03°04^,13'

*20 J

Po tych wstępnych wyznaczeniach, należy ustalić równania poprawek do wyników pomiaru, a na tej podstawie - elementy macierzy A i L. Konkretne postaci tych równań ustalimy korzystając z ogólnych równań poprawek, adaptując je do poszczególnych szczegółowych sytuacji geometrycznych i warunków zadania. Zatem:

- dla boków

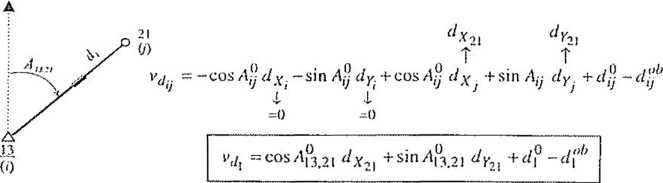
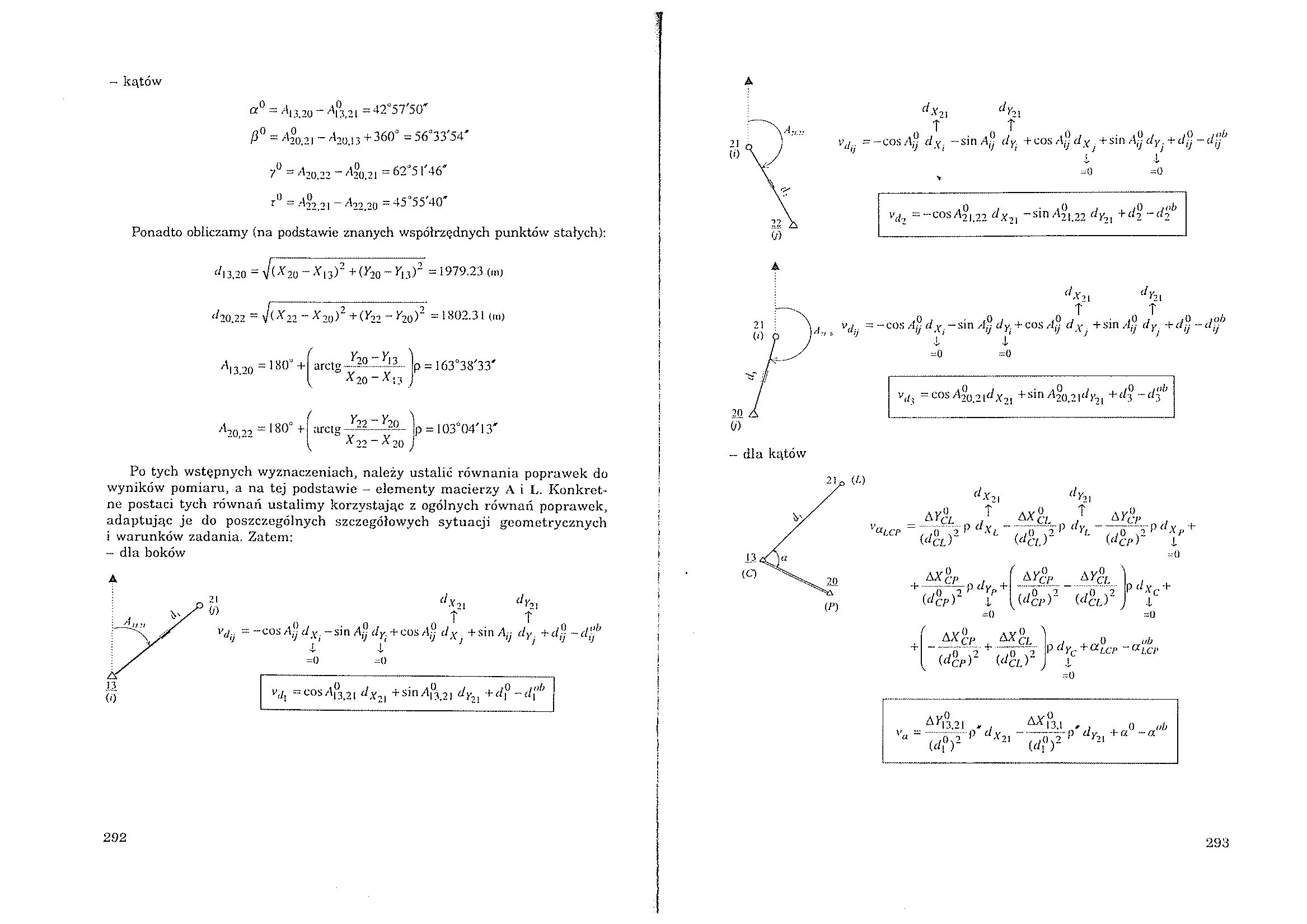
^ciX_2]    ^(lY_2X

T    T

v_t[ ~ -cos A-j dYj —sin Ay dy. + cos Ay dy ^ + sin Ay d_Y. + djj - dy

-0

^vci-, ~ “•COS/to 1.22 ^dX->_x ~sin An|.22 ^dYn; + d₂ -d

^dx_n    ^dr_n

T    f

^vdjj ⁼ “ djj d y. — sin Ajj dy. + COS Ajj d y . + sin Ay (ly. + djj •

X    X

^0    =0

v_(/, =COSA20.2I^X_2! +sin ^20,21    ^{+ d}'i ~^dl’

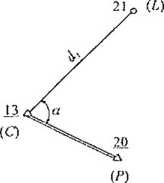
„    - Jil.ę.k

^ULC!> (dę_L)

AX

⁺ 71ó

⁽ⁱX₂\    ^(lY₂ i

AYę_L ?    AX⁽h ^T    AY^>

c. _p    jp ,/_Kf --------

Wcl)    (^a.)

, , f _ ^aycl ^

, ,0    2^P</y'/^>+    ,.0 x2    v2 ¹

(“Cf>) i ^ ("C7^ł)    («Cl) j

P^x,

04r)

AX ęp    AX y-; 'j    o

-----_p </>,+« -a

>² .^c

W ■ «&.>*;

AK,

13.21 , ,    '-^13,1 * ,    o ab

293