297 (7)

1

■ )

się związ-!orminują j

unkcic do j

tgar,

5.2f.)

llJ.2. Związek pochodnej funkcji z monotonicznoicią i ekstremum funkcji (I)

[włiodna a monotoniczność funkcji - wnioski z twierdzenia La-'jringea(por. U.2.2.el)

jjieli funkcja y=f(x) jest różniczkowalna w pewnym przedziale (ograniczonym lub nie), to dla dowolnego x z tego przedziału mann- nasiępujijce związki między pochodną a monotonicznością fuńkcjiw tym przedziale:

I- f'(^x) > 0 =»/f

III. f'(x) = 0 -*/const

Uwaga: Przy ww. założeniach zachodzą ponadto następujące implikacje:

//-/■(*)>()

•iftrbodna a ekstremum funkcji

H Warunek konieczny istnienia ekstremum funkcji różniczkowal-

I

jadi funkcja y = /(,v) jest różniczkowalna w punkcie r₀imaw tym fmkae ekstremum, to f'(x₀) = 0:

lf ma w x₀ ekstremum)    =>    (f(^xo) ⁼ o)

nranek wystarczający    warunek konieczny

por. Uwaga w: 1.1.2.

a monolonltinośC I okstromum

tne zadała ponad ąż swego jeometrii dmiotem stanowi alalności

anika kla-yczerpuje podstawy

Uwaga 1: Warunek f(x₀) = 0 (jako następnik implikacji) to warunek konieczny, ale nie wystarczający dla istnienia ekstremum, na przykład rozwiązując równanie /'(*„) = 0 dla funkcji y = x^>:3x²= 0, otrzymujemy r=Q. Ale w x = 0 funkcja y = x nie u ekstremum w x₀, mimo że f(i,)=/(0) = 0 - czyli warunek taneczny jest spełniony, ale to nie •ystarcza, gdyż warunek zerowania * pochodnej nic jest warunkiem *J8arczającym na ekstremum, taaga 2: Jeżeli/mawz₀ pochodną rótną od zera: /'(*„) # 0, to / nie “w z, ekstremum:

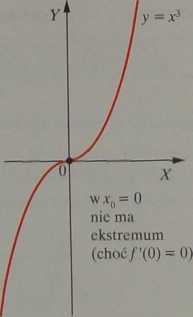
/'(*„) #0 •» w x₀ nie ma ekstremum

W. 1.1,3, - prawo transpozycji)

Stefan Banach (1892-1945) -jego twórczość przypada na okres, w którym żyło i tworzyło wielu stawnych

matematyków polskich. Z dorobkiem tego okresu wiąże się działalność polskiej szkoły matematycznej, która zdobyła mię-dzynarodowc uznanie.

Praca akademicka Banacha datuje się od roku 1920. Objął wtedy stanowisko asystenta na Politechnice Lwowskiej. Od tej pory rozpoczęła się jego kariera naukowa. W tym samym roku przedstawił na Uniwersytecie Lwowskim pracę pt.

O operacjach na zbiorach abstrakcyjnych i ich zastosowaniach do równań całkowych. Miała ona pierwszorzędne znaczenie dla analizy funkcjonalnej. Oceniono ją wówczas wysoko, skoro nadano mu stopień doktora, mimo że nie miał ukończonych studiów wyższych. W roku 1939 uzyskał nagrodę Polskiej Akademii Nauk Umiejętności oraz został wybrany dziekanem na Uniwersytecie Lwowskim i prezesem Polskiego Towarzystwa Matematycznego.

Ten samouk do historii matematyki wszedł jako główny współtwórca analizy funkcjonalnej, zwanej także teorią operacji. Podstawowe pojęcie tej dyscypliny matematycznej stanowi „Przestrzeń Banacha”, a do podstawowych opracowań w tej dziedzinie należy główne dzieło Banacha - Teoria opera-cji. |

Nie lubował się w dociekaniach logicznych, choć rozumiał je doskonale. Nie pociągały go także praktyczne zastosowania matematyki.

U. CIĄGŁOŚĆ I POCHODNA FUNKCJI