3 (1249)

Edukacja - Mozilla Firefox

Plik Edycja Widok Historia Zakładki

0 - c x & »

Narzędzia Pomoc

\_/ (ł 0 E https://edu.pjwstk.edu.pl/result2.a$p?id=1034		Google	P

Allegro l) BPH ±\ Damoria H Darkwarez Q Desert Operations [2] Edu Pjwstk l] Epg M Grnail ^ Google >^NI Interia Koleje Mazowieckie Q Kurnik 0 Nasza klasa

Onet H] PAYBACK □ Poczta PJWSTK Q SQL ^ Teksty & Torrenty £*3 Wirtualna Polska

J Edukacja    |    |_[j*-

MENU    TESTY2    ZatogcwBiy.HtełałPteeK KirrAfcior^UttiKtwdaryct (ASP)    POMOC    WYLOGUJ

H Kurs **! Wykłady >/ Oceny Materiały B Foldery zadań |7 • Forum ii; Chat Bj'>) Ogłoszenia

[s7] Kalendarz O FAO Lekcje % Testy 2 PI Zadania [_j Bibliografia W Inny kurs O Wyloguj ^ Administrator

Zakończono

/; Start

Twój wynik: 3 punktów na 6 możliwych do uzyskania (50 %).

Piwek Michał

_^_

Opcja

Punkty

Poprawna

i Odpowiedź

Do znalezienia elementu największego w danym n elementowym ciągu, gdzie n jest potęgą 2, zastosowano następujący algoiytm

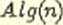
•    jeżeli ciąg składa się z jednego elementu, to jest to element największy,

•    jeżeli ciąg składa się z więcej niż jednego elementu, to dzielimy go na połowy, w każdej z nich rekurencyjnie wyszukujemy element największy, porównujemy uzyskane wartości i ustalamy ostateczny wynik.

Które z poniższych zdań jest prawdziwe?

	Funkcja rekurencyjna ^ (0 ^_ ^O^1) ^_ 2T(n 1) 1 ^ jest równaniem złożoności czasowej rozważanego algorytmu	0		+
	T(Alg,n) = ć>( 2^n)	0		+
	S(Alg,n) = @(n)r uwzględniając koszt pamięciom wywołań rekurencyjnych	1	+
	Ile porównań elementów wykonuje algorytm Alg(n)
	1.    inti:=n; 2.    while(i>l)do
2	3.    P(r); 4.    i:=i-l; 5.    od
	jeżeli ^^J(^l) jest optymalnym algorytmem wyszukiwania największego elementu w i elementowym zbiorze nieuporządkowanym?
	n	0
	0(n*)	1	+
	Liniowo dużo względem n	0		+
3	J aką pozycję zwróci algorytm Partition (pozycje ciągu numerujemy od 1, a jako element rozdzielający wybieramy ostatni element rozważanego ciągu)?
	Jeżeli ciąg jest postaci lJ2I3,...,100j to wynikiem jest pozycja 100	1	+	+
	Zawsze jest to k -ta pozycja, gdzie - S^n i n jest długością ciągu	1	+	+
	Zawsze jest to -/TT pozycja, gdzie n jest długością ciągu	0
4	Koszt algorytmu Partition, zastosowanego do ciągu o n elementach jest:
	^(^9^n), jeżeli operacją dominującą jest porównanie elementów	0
	Rzędu n, jeżeli operacją dominującą jest przestawienie elementów	0
	Rzędu n, jeżeli operacją dominującą jest porównanie elementów	1	+	+
5	Miech P będzie problemem wyszukiwania elementu £-tego co do wielkości w danym n-elementowym zbiorze. Które z poniższych zdań jest prawdziwe?
	Jeśli k = n, to problem można rozwiązać z kosztem n 1	1	+	+
	Jeśli k = 1, to problem można rozwiązać z kosztem	0		+
	Jeśli k = 3, to problem można rozwiązać wykonując co najwyżej ra-p/ęn—3 porównania	0
ó	Rozważmy tablicę T reprezentującą 9-elementowy ciąg różnych liczb naturalnych: 0,12,17,13,10,14,2,9,11 \;y 0wej tablicy wyszukujemy indeksu elementu 9- go co do wielko ś ci za porno cą algorytmu Ho are^1 a z procedurą po działu zgodną z metodą Partition. Które z poniższych zdań jest prawdziwe?
	W rozważanym przypadku liczba wykonanań algorytmu Partition jest większa od liczby wykonań tego algorytmu, gdy zamiast indeksu elementu 9-go co do wielkości będziemy wyszukiwali indeksu elementu 2-go co do wielkości	1	+	+
	Argumentem I-go wykonania algorytmu Partition jest tablica postaci: [0,12,17,13,10,14,2,9,ll]? w której szukamy indeksu elementu 6-go co do wielkości	0
	W rozważanym przypadku liczba wykonanań algorytmu Partition jest równa dokładnie 3	0

S>s*w ectkactfrty. P-jWSTK 2M1-2007

?’) Edukacja - Mozilla Fir...

>t: 2-Paint

* / *
Lii! 0 O Aktualna pogoda: Zachmurzenie umiarkowane, -2 °C	Pon: 3 °C (P^J>	Wt: 5 °C <0

ES ^f< j& 'Q 20:54