51 (314)

51

łających liczby pomiarów w przedziałach do całkowitej liczby pomiarów. Rozkład tych częstości występowania w całym zakresie zmienności nazywamy rozkładem empirycznym zmiennej losowej. Rozkład teoretyczny zmiennej losowej jest to rozkład prawdopodobieństw występowania wszystkich wartości zmiennej losowej w całej populacji. Gdybyśmy dysponowali dużą liczbą wyników pomiarów pewnej wielkości, wówczas zarówno wartość rzeczywista mierzonej wielkości, jak i rozproszenie charakteryzujące stosowaną metodę pomiaru można by łatwo wyznaczyć z empirycznej krzywej rozkładu wyników pomiarów.

Przykład 2.2    |

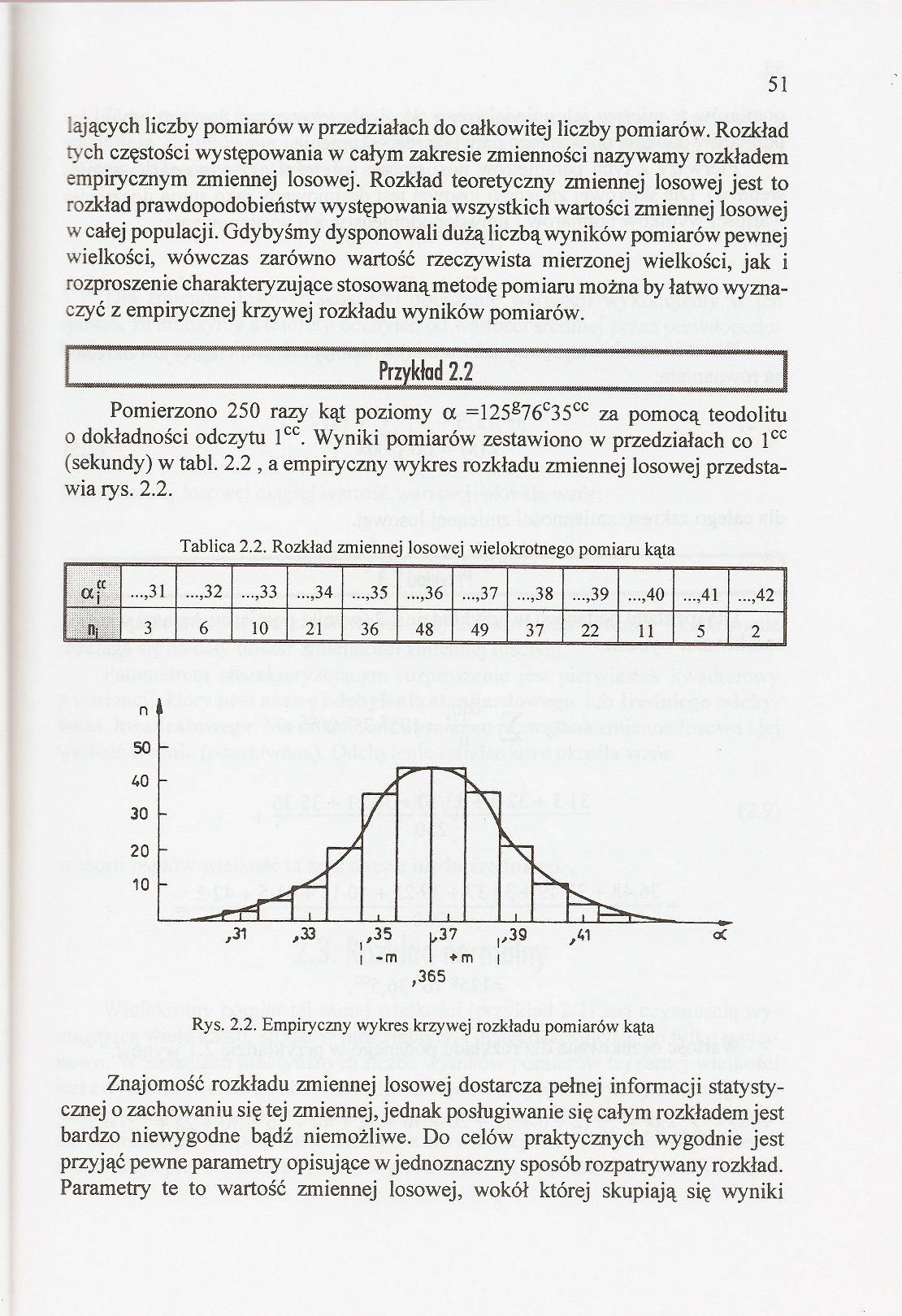
Pomierzono 250 razy kąt poziomy a =125^g76^c35^cc za pomocą teodolitu o dokładności odczytu l^cc. Wyniki pomiarów zestawiono w przedziałach co 1°® (sekundy) w tabl. 2.2 , a empiryczny wykres rozkładu zmiennej losowej przedstawia rys. 2.2.

Tablica 2.2. Rozkład zmiennej losowej wielokrotnego pomiaru kąta

■«r	.....31	...,32	...,33	...,34	mm	...,36	,..,37	...,38	...,39	...,40	...,41	...,42
"i	MW	6	10	21	36	48	49	37	22	11	5	2 .

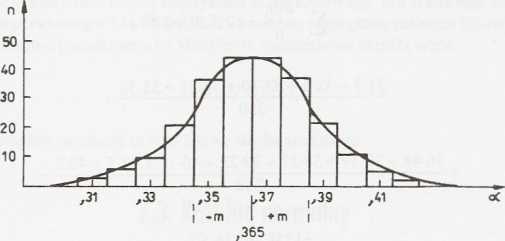
Rys. 2.2. Empiryczny wykres krzywej rozkładu pomiarów kąta

Znajomość rozkładu zmiennej losowej dostarcza pełnej informacji statystycznej o zachowaniu się tej zmiennej, jednak posługiwanie się całym rozkładem jest bardzo niewygodne bądź niemożliwe. Do celów praktycznych wygodnie jest przyjąć pewne parametry opisujące w jednoznaczny sposób rozpatrywany rozkład. Parametry te to wartość zmiennej losowej, wokół której skupiają się wyniki