CCF20130102�108
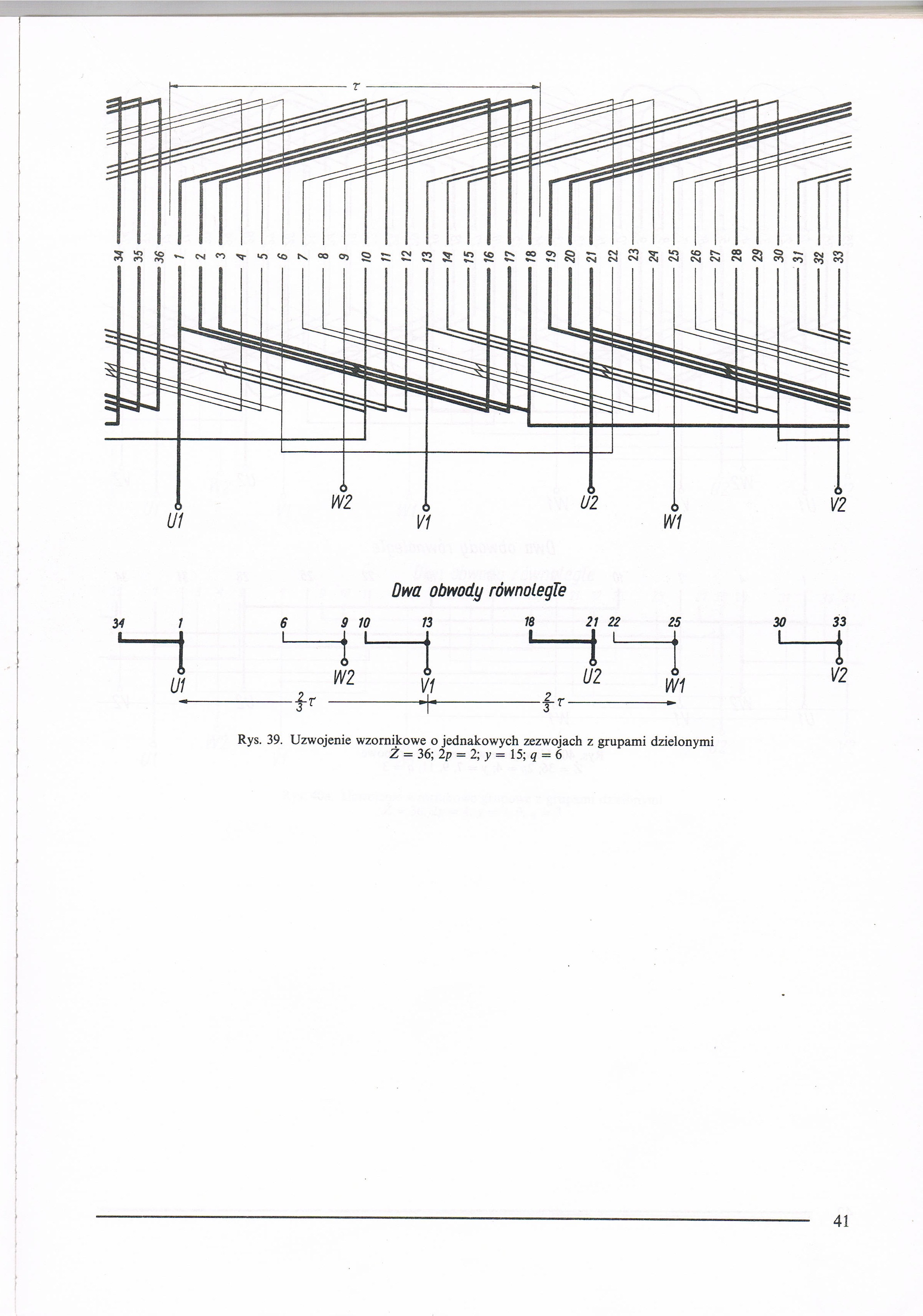
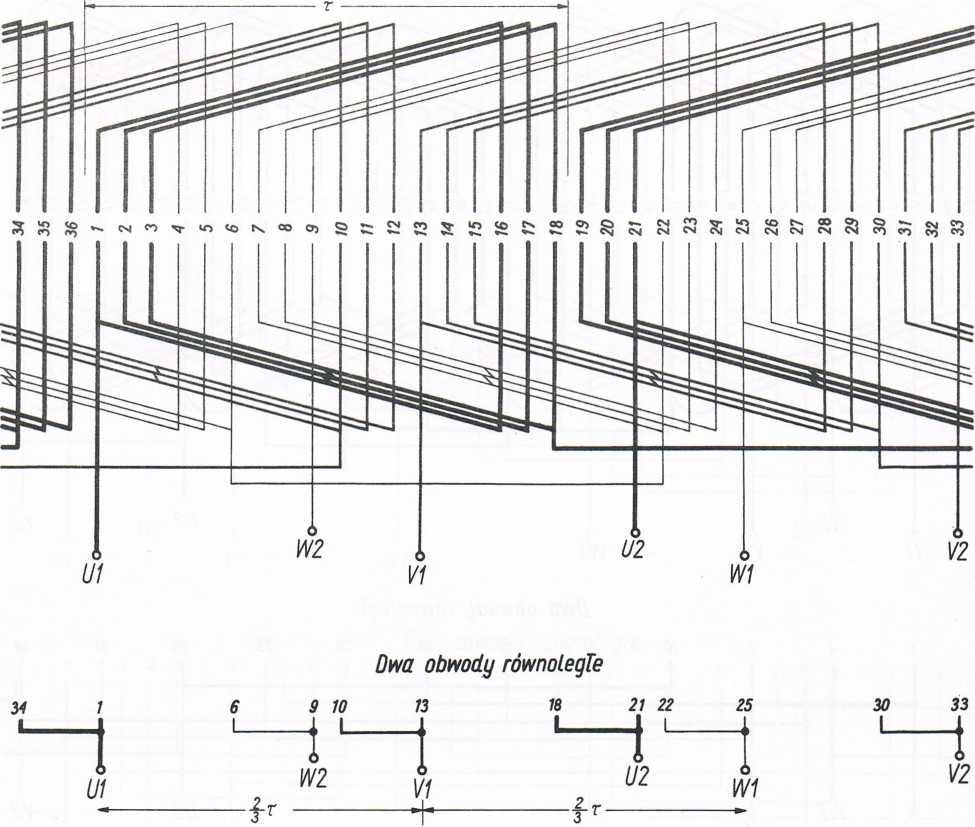
Rys. 39. Uzwojenie wzornikowe o jednakowych zezwojach z grupami dzielonymi Ż = 36; 2p = 2; y = 15; q = 6
Wyszukiwarka
Podobne podstrony:
CCF20130102�103 Rys. 33b. Uzwojenie wzornikowe o jednakowych zezwojach Ż = 18; 2p = 2; y = 9; ą = 3
CCF20130102�124 L/ Rys. 53. Uzwojenie wzornikowe o jednakowych zezwojach Ż = 54; 2p = 6; y = 9; ą =
CCF20130102�111 Dwa obwody równolegle Rys. 41. Uzwojenie wzornikowe o jednakowych zezwojach Ż = 36;
CCF20130102�104 Rys. 34a. Uzwojenie wzornikowe grupowe z grupami dzielonymi Ż = 24; 2p = 2; y = 9, U
CCF20130102�110 Dwa obwody równolegle Rys. 40a. Uzwojenie wzornikowe grupowe z grupami dzielonymi Z
CCF20130102�122 Rys. 51. Uzwojenie wzornikowe grupowe z grupami dzielonymi Z = 54; 2p = 4; y = 9, 10
CCF20130102�131 Rys. 60. Uzwojenie wzornikowe grupowe Ż = 90; 2p = 10; y = 7, 9, 11; q = 3
CCF20130102�147 oo o Rys. 72a. Uzwojenie dwuwarstwowe z grupami dzielonymi Ż = 36; 2p = 2; y = 12, 1
CCF20130102�077 Rys. 6. Połączenie czołowe uzwojeń wzornikowych kowych zezwojach oraz u z w oj e n i
CCF20130102�130 ON U) Rys. 59. Uzwojenie wzornikowe grupowe z grupami dzielonymi Z = 90; 2p = 6; y =
CCF20130102�087 Dwa obwody równolegle Rys. 19. Uzwojenie trzypiętrowe równogrupowe z grupami dzielon
CCF20130102�089 Ul V1 W1 Rys. 21. Uzwojenie trzypiętrowe równogrupowe z grupami dzielonymi Ż = 54; 2
CCF20130102�099 Rys. 31. Uzwojenie trzypiętrowe równogrupowe z grupami dzielonymi Ż = 90; 2p = 6; y
CCF20130102�102 2.1.2. Uzwojenia wzornikowe Rys. 33. Uzwojenie wzornikowe grupowe Ż= 18; 2p = 2; y =
CCF20130102�112 Trzy obwody równolegle Rys. 42. Uzwojenie wzornikowe grupowe Ż = 36; 2p = 6; y = 5,
CCF20130102�128 rUlVI wTrzy obwody równolegle Rys. 57. Uzwojenie wzornikowe grupowe Z = 72; 2p = 6;
CCF20111125�001 (3) i •• Rys. 63. Uzwojenie klatkowe wirnika maszyny indukcyjnej / - pręty, 2 - pier
CCF20130102�134 Rys. 64. Uzwojenie koszykowe Z = 36; 2p = 6; y = 5; q = 2 Rys. 64a. Uzwojenie koszyk
CCF20130102�135 Rys. 65. Uzwojenie koszykowe Ż = 48; 2p = 8; y = 5; q = 2
więcej podobnych podstron