DSC00074 (19)

4,1 cP /4,1.10"^

m

2,7 cP /2,7.10“³

lepkość w 80°C ,u =

lepkość w 100°C ął_s=

Temperatura ściany zewnętrznej wężownicy wynosi 100°C. E.o związanie Znajdujemy liczby Reynoldsa i Prandtla

⁵<m=

n.L².i

120,

/§0^x|g^ZZ2^810 _ 30₅₂₀₀

17,67

* . 2600^ . ^oo^^si

Określany liczbę Nusselta z zależności

Ru = 0,87 /£/^0,14.Re°*⁶².Pr°»³³

Hu | 0,87 /2^/^0,14.305200⁰»⁶².17,67^0,33=524O

Z liczby Husselta znajdujemy «

oc I iiHii I ?24O.0_a^24 I 1220 kcal/m².h.°C /1415    -/

7*    •    m².grad

Zadanie 4,

Obliczyć współczynnik konwekcji przy przepływie alkoholu metylowego w przestrzeni międzyrurowej wymiennika przepo— aowo-rurowego z poprzecznymi przegrodami. Zewnętrzny prześ -v.it rur d | 25 mm. Natężenie przepływu alkoholu W = 168 -jr²— * średnia temperatura t | 37,7°C. Stałe fizyczne alkoholu ^m*^se metylowego w tej temperaturze są następujące:

lepkość    = 0,465 cP /0,465.10“³ &4§f|

O -    ^ w

przewodnictwo wł. % | 0,179 kcal/m. C.h /0,208

u • gX’cLQ

ciepło właściwe c | 0,634 kcal/kg.°C /2656 gg^rad^

Rozwiązanie

Znajdujemy liczby Reynoldsa i Prandtla

Re

d.u.i

^•S

fllgS | 9050

_Pr | 2600.^ | 2600^0^^.?,81 1 _5i9

Określamy liczbę Ilusselta z zależności obowiązującej dla przenikania ciepła od cieczy do wiązki rur, jeśli omywanie rur jest kierowane poprzecznymi przegrodami

Ku = 0,2.Re⁰,6.Pr°»⁵⁵ = 0,2.9050°*^e    = 86,9

Znajdujemy oc

cc =

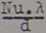
0.179.86,8

0,025

= 620 kcal/m².h.°C /719 ^-—3/

ZscłflTłl6 2 •

Obliczyć współczynnik konwekcji dla zewnętrznej powierzchni rur chłodnicy, zraszanej z zewnątrz wodą. średnica zewnętrzna rur 76 mm. Odległość w pionie pomiędzy osiami rur 160 mm, długość rur | m. Zużycie wody chłodzącej 4000 kG/h, temperatura wody 20°C. W tej temperaturze lepkość wody 1 cP IIP    ciężar właściwy 1! = 1000 kG/m^, ciepło

właściwe wody 1 kcal/kg. C /4-190 ■■—-■ /,

kg. C

A= 0,515 kcaVm.h.°C /0,597 ₅Jfaa^/ł

Rozwiązanie

Współczynnik oc wyznaczymy z zależności

Nu = 0,005 Re^0,4.Pr⁰*⁴

W tym celu określimy najpierw liczby Re i Pr.

Biorąc pod uwagę ściekanie cieczy na obie strony rur - gęstość zraszana wynosi    0

p =    = 400 kG/m.h

1

65