DSC00278 (16)

4 t

CD

Potencjał pola elektrostatycznego

f‘ !cr# * -i po i danym punktu jest stosunek energii potencjalnej ładunku q . którą mialhr, _lt ' •    » tym punkcie, do U go ładunku, i * ~~

/ ił * i . [> ,T..r, ;.ilu juvi wolt t - FV>lc elektrostatyczne ma u danym punkcie potcnq.il \\ _y **■    ■ ■ . n -u ^r c f. lorka .« z mcNkonczonoset do tego punktu silą zewnętrzną musi wykon a pracę l i

- P* ^v- i ' * poi. centralnc.:o zalczy t>d (Kllcglosei tego punktu od żriklla pola. jest wielko-

¹ dc* ki/tt,.! k^r r i n /.. pr/yin.owae wartości dodatnie, jak i ujemne

praca pr

potencjału

padłe do d U - /

linie

I)

ULJ

Jf U na *su»r/4)ąty pt*łc

i * pole ixjut

Jf/tli ładunek wytwarzający pc»lc jest ujemny to potcncjid w dowolnym punki ic tego poła jest również ujemny

•^c/'-ł •    J⁴- *' 'Aurzonc pr/c/ wiele ładunków punktowych Q_v Q_v Q to potencja! w dowolnym

I ^: ' ^J • ^,( K ¹ p a /r luje. n> stosując / isadę superpozycji Jest on sumą algebraiczną potencjałów wytwarzanych pr/c/ poszczególne punkty: V = V ₍+ l' +    + V_ą.

Napięcie

potcncjahiiw mi^d/y dwoma punktami pola «    ^;    * l nazywamy napięciem mię

dzy lyiro punktami i oznaczamy literą Ł/_t £/ = V_A- l .

Si * /cwnętr/i równoważąca w każdym punkcie to-

r i vdc poJa pr/ .V. : ac ładunek «/ (dodatni) z punktu /t do /?, wykonuje dodatnią pracę W =f. - £_r powoduje w zrost energii potencjalnej ładunku Ponieważ E_p= l </₍, to wzór na pracę możemy zapisać

W

i s;i prosu tyczne zw wnętr/nc na metak pól elekti osłony uz rowych, ł osłonę pi oraz pow

%

H

A

U

<1 „(1,-1 JlublV,    ,= -^

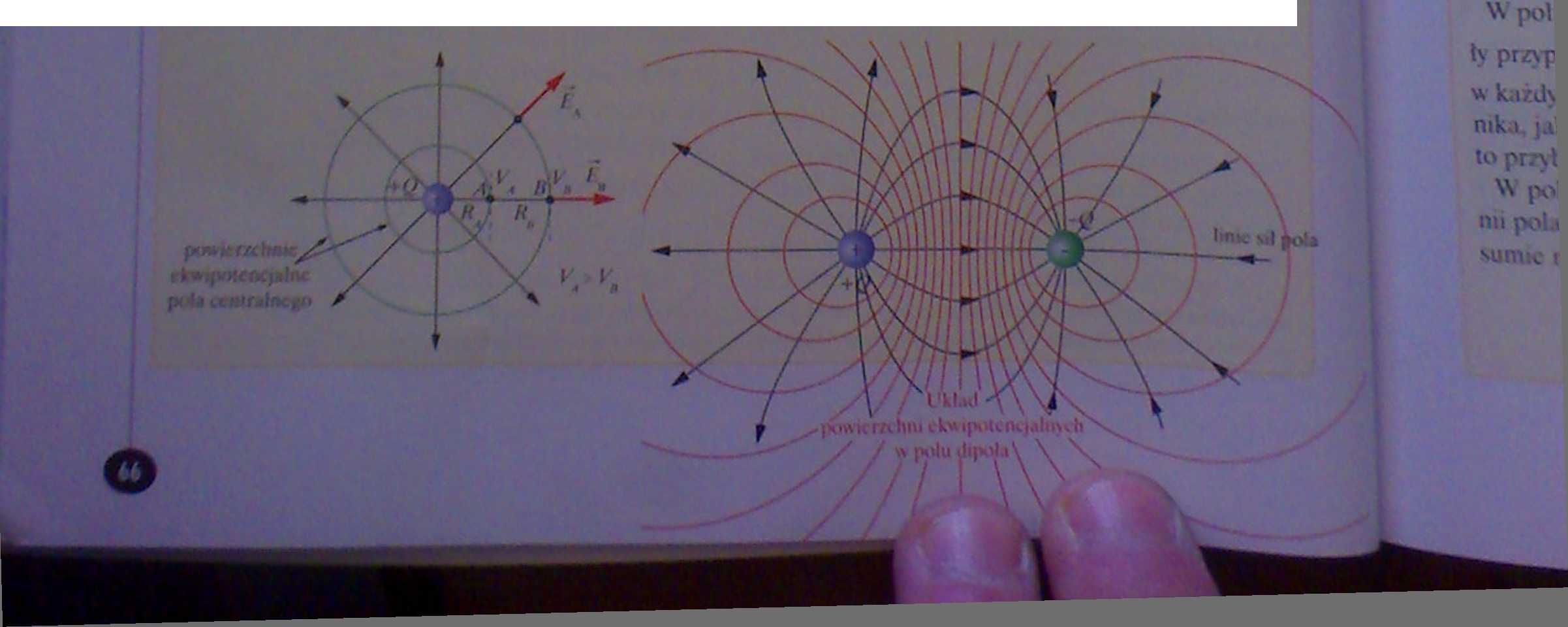
Powierzchnie ekwipotencjalne (I)

'• ’ punk? c/ącc na powierzchni kulistej o promieniu R_t w której środku znajduje się I idunck jnl tow* Q (\*)k centralne i maja len sarn potencjał. Powierzchnia równego potencjału zwana jest powierzchnią tkwipotcncjalną

br.via/.!.:i i tkwipołcncjalna jesl w każdym punkcie prostopadła do wektora natężenia pola W polu uki :tJu Udunlcow punkfnwych mc kulistych ciał n ac lek t ryzowanych powierzchnie ekwipotencjalne pr/\|mu j i rroznorodmejs/e k złalty