DSC03936

310

przegląd najczęściej stosowanych anten

ANTENY MIKROPASKOWE

311

mogą zostać określone poprzez rozwiązanie równania Helmholtza dla jednorodnej wnęki rezonansowej przy zerowych warunkach brzegowych. Amplituda pola nie może być określona tylko na podstawie samej wnęki. Jeśli założymy, że dielektryk wewnątrz rezonatora wnękowego jest bezstratny, to analiza wykaże, że impedancja wejściowa jest czystą reaktancją. Wynik ten stoi w sprzeczności z pomiarami — impedancja wejściowa anteny mikropaskowej ma część rzeczywistą odpowiedzialną za promieniowanie energii w przestrzeń.

Dla dominującego rodzaju rezonansowego pole elektryczne w kierunku osi z może być określone jako

E* = EoCOSy^-    (11.100)

natomiast pole magnetyczne jako

H_y = Hq sin—    (11.101)

Rodzaje rezonansowe wyższych rzędów mają więcej zmian wzdłuż osi x i/lub osi y. Rezultat ten nie uwzględnia deformacji pola występującego na krawędziach promiennika, tak więc konieczna jest poprawka długości rezonansowej w celu otrzymania dokładnej częstotliwości rezonansu anteny.

Model anten mikropaskowych uwzględniający strukturę podłoża i prawdziwy dla każdej częstotliwości jest zwany modelem pełnofalowym. Zakłada on, że podłoże wraz z płaszczyzną masy mają nieskończone wymiary. Jest to w zasadzie jedyne ograniczenie teoretyczne, które w praktyce nie ma większego wpływu na obliczone parametry (za wyjątkiem charakterystyki promieniowania). W modelu pełnofalowym przyjmuje się odpowiednie warunki brzegowe na granicy dielektryków między warstwami lub na granicy dielektryk — powietrze. Model wykorzystuje funkcje Greena dla dielektryków wielowarstwowych, które pozwalają uwzględnić promieniowanie anteny, wzbudzanie się fal powierzchniowych, straty w dielektryku oraz wzajemne sprzężenia między elementami. Użycie funkcji Greena w połączeniu z metodą momentów daje w rezultacie bardzo dokładny opis, który znajduje zastosowanie do praktycznie wszystkich możliwych struktur anten. Kosztem, jaki płaci się za wysoką dokładność i uniwersalność, jest duży poziom komplikacji i wymagana bardzo duża moc obliczeniowa komputerów. Cechy modelu są następujące:

•    dokładność — model pełnofalowy dostarcza naj dokładniej szych wyników przy obliczaniu parametrów anten (impedancja wejściowa, wzajemne sprzężenia itd),

•    zupełność — model obejmuje wszystkie zjawiska fizyczne, takie jak efekt fal powierzchniowych, wzajemne sprzężenia między elementami, promieniowanie anteny, straty w dielektryku i przewodnikach itp.,

•    uniwersalność — model można zastosować do arbitralnie narzuconych struktur i układów antenowych, różnych sposobów zasilania, układów wielowarstwowych i anizotropowych,

•    złożoność obliczeniowa -— model pełnofalowy wymaga największej mocy obliczeniowej (obok modelu opartego na technice FDTD) spośród wszystkich wymienionych tu modeli oraz wymaga szczególnie starannej algorytmizacji i programowania w celu zwiększenia efektywności kodu.

Inna obiecująca metoda analizy jest oparta na technice FDTD (Finite Difference Time Domain). Wymaga ona bardzo dużych mocy obliczeniowych i zasobów komputera, co praktycznie ogranicza obecnie od dołu częstotliwość analizy anten, jednak przy ciągłym postępie w budowie szybkich komputerów to ograniczenie wkrótce przestanie być istotne. Metoda FDTD nie narzuca żadnych ograniczeń na strukturę geometryczną anteny. Charakterystyka promieniowania w strefie dalekiej jest obliczana za pomocą transformaty Fouriera pola w otoczeniu anteny (strefa bliska).

Wspomaganie procesu projektowania anten za pomocą programów komputerowych jest zagadnieniem bardzo istotnym. Skraca ono czas potrzebny na wykonywanie kolejnych modeli, a także obniża koszty całego procesu. Ostatecznym potwierdzeniem symulacji komputerowych wykonanych w procesie projektowania jest jednak zawsze budowa i pomiar rzeczywistego modelu anteny.

Uproszczone projektowanie anteny mikropaskowej o kształcie prostokątnym polega na określeniu częstotliwości rezonansowej i właściwym dobraniu materiału dielektrycznego (laminatu) o przenikalności względnej e_r. Długość rezonansowa L (rys. 11.86) może być obliczona z przybliżonego wzoru [15]

L = 0,49    (11.102)

V ^er

Impedancja wejściowa na krawędzi łaty (x = 0) wynosi [15]

i ^z--⁹⁰Tr§r(#)’

Impedancja wejściowa maleje zatem przy poszerzaniu łaty. Zbyt szeroka łata może jednak spowodować wzbudzanie się wyższych rodzajów pola w antenie. Można wtedy dopasować impedancję poprzez wycięcie wzdłuż linii mikropaskowej szczeliny o długości x, która redukuje impedancję o czynnik cos² (x • n/L), choć przy dużych wartościach x (anteny wykonane na podłożu o dużej przenikalności) pogarsza się charakterystyka promieniowania i rośnie promieniowanie o polaryzacji ortogonalnej.

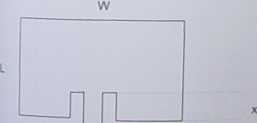
Rys. 11.86. Rozmiary geometryczne prostokątnej anteny mikropaskowej