DSC07030 (4)

48

^c»*gł

b)    Zbiór punktów skupienia ciągu (yn) ma postać S = {—l,co}, zatem

Jim z_n = —1    oraz    lim Zn = oo.

"-⁰⁰

c)    Zbiór punktów skupienia ciągu (zn) ma postać 5 = |-2, ~,0, i, 1, |J, zat^ |

P" 3

lim Zn — ”2    oraz    lim Zn = -.

n=S>    ⁿ-°°    ²

d)    Zbiór punktów skupienia ciągu (u>») ma postać S = {-oo.O.oo}, zatem

lim uin = -oo    oraz    Bm w_n = oo.

n^oo

Zadania

• Zadanie 1.1

Na podstawie wartości kilku początkowych wyrazów podanych ciągów znaleźć ich

wzory ogólne:

^a) (^zn) —(1,2,6,24,120,...); c) (Zn) = (1,3,7,15,31,63,. «) (°n) = (1,4,7,10,...);

g) (c.) = (0,1,0, -1,0,1,0, -1,...); i) (e.) = (0.7,0.77,0.777,0.7777,...);

b)(y„)=(i.i^|3,J,5,i, -); d) (t_n) = (1,1,1,2,2,2,3,3,3,...); g f) (6„) = ($, -4\/2,‘l, —2v/§, -.‘

h) (dn) = (0,1,5,23,119,...);

J*) (/») = (0,1,1,0,0,0,1,1,1,1,...).

• Zadanie 1.2

Dla podanych ciągów napisać wzory określające wskazane wyrazy tych ciągów:

»)««="".    ^b)»»⁼^⁺2^rr⁺ra⁺ --⁺3^’^!,n+i:

c) Zn = (2n + 1)!, in+j; d) In = (n³ + l)³,

e) On = V"¹ + 1, o«+j; g)c.=(nO"‘. d,„

|^Ł"⁼(jS ^63n+S:

h)d_n = 3ⁿ + 3ⁿ⁺¹ + ... + 3^,n, c_B,.

• Zadanie 1.3

Zbadać, czy podane ciągi są ograniczone z dołu, z góry, są ograniczone: ,)z_n=n⁴~n³;    b) y_n = (-l)"n!;

c)

e) On

d) tn

(-2)ⁿ 1 + (-2)"’

y/rT+H - Vń+3;_f) *»„ = 2ⁿ - 3";

Zadania

49

₊»B^{1 1}

s) ^    ⁴³⁺³

- ^nTr s¹\ _P - Bi

h) dn = 2 ^s,n“5"’    ‘ ^{J n} n!¹

+ ...+

4" +

• Zadanie 1.4    . .

Zbadać czy podane ciągi są monotomcznc od pewnego miejsca:

a) ¹» = "a _6n+U)’

I00?r .

^c)an=fcB^1,

e)o„ = n²-49n-50;

_v n^a.

g) °n 2” ’

_ 2" + 1.

0 e»- 3n ₊ 1'

^b) yn =

4"

2ⁿ + 3ⁿ’

■.¹§4

0 b_n = 3ⁿ + (-2)ⁿ;

¹    47....(l + 3ny

i) /n = Vn³ + 2 - n.

Zadanie 1.5

Korzystając z definicji granicy właściwej ciągu uzasadnić podane równości¹.

= 0;

a) lim    = 0;

' n—00 n²

c) lim ——— = -1; n—OO n + 4

_b)

⁹ n-00 2ⁿ + 3"

^d) -¹”⁹- FTś

') lim    ₌₂. f.) _Um iM=₀.

n—00    \ n + 1 /    ' n-¹oo n!

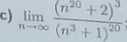
d) Um

tf8^nVf + 3

n—00 2" + 1

^e)    o «■>. (v^Ti-Iffi+S):

n—00 »/

Ujgil

1

   Zadanie 1.6

Korzystając z definicji granicy niewłaściwej ciągu uzasadnić podane równości:

^a) _n^,”5₀^°S2(ⁿ⁺³) — co¹. b) łiin^ (n⁴ - 1) = 00;

^c) bjL (n/^ ~ n) ~ -co; d) lim (10—>/n) = -oo.

n—¹00

•    Zadanie 1.7

Korzystając z twierdzeń o arytmetyce granic ciągów obliczyć podane granice:

al Um (ł/nTjTw! _Y ..... (n’ + l)n! + l.

^+l6 J’ ^b)n^b™oo(₂V+Y)(^+ij!’