DSC09119
| Rozwiązanie:
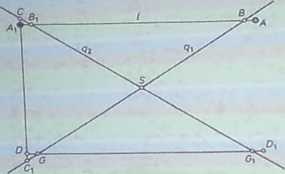
i2. Przez punkt Al należy poprowadzić inną dowolną prostą. Przecina ona proste ql i q2 odpowiednio w punktach C oraz Cl. Leżący symetrycznie wobec punktu At punkt D jest punktem należącym do lewej gałęzi poszukiwanej hiperboli.
Wyszukiwarka
Podobne podstrony:
DSC09120 Hiperbola o zadanych asymptotach i danym punkcie Rozwiązanie: 3. Przez punkt Aj należy popr
DSC09120 Hiperbola o zadanych asymptotach i danym punkcie Rozwiązanie: 3. Przez punkt Aj należy popr
DSC09121 Hiperbola o zadanych asymi I Rozwiązanie: I 4. Przez punkt K należy poprowadzić I dowolną p
DSC09121 Hiperbola o zadanych asymi I Rozwiązanie: I 4. Przez punkt K należy poprowadzić I dowolną p
DSC09092 Rozwiązanie: 2. Przez środek 5 okręgów jrt i należy poprowadzić dowolną prostą ę. Prze
DSC09092 Rozwiązanie: 2. Przez środek 5 okręgów jrt i należy poprowadzić dowolną prostą ę. Prze
DSC09110 Rozwiązanie: 3. Wykorzystując konstrukcję symetralnej odcinka należy wyznaczyć środek
DSC09110 Rozwiązanie: 3. Wykorzystując konstrukcję symetralnej odcinka należy wyznaczyć środek
DSC09117 Hiperbola o Udanych asymptoUch i danym punkcie Rozwiązanie: 1. Przez punkt A należy poprowa
DSC09118 “danych asymptotachI danym punkcie Rozwiązanie: 1. Przez punkt A należy poprowadzić do
DSC09117 Hiperbola o Udanych asymptoUch i danym punkcie Rozwiązanie: 1. Przez punkt A należy poprowa
DSC09118 “danych asymptotachI danym punkcie Rozwiązanie: 1. Przez punkt A należy poprowadzić do
DSC09093 ! Rozwiązanie: 3. Przez punkt 1 należy poprowadzić prostą prostopadłą do oś AB, przez&
DSC09111 Rozwiązanie: 4. Ze środka w punkcie O należy wykreślić okrąg jr przechodzący przez pun
DSC09093 ! Rozwiązanie: 3. Przez punkt 1 należy poprowadzić prostą prostopadłą do oś AB, przez&
DSC09111 Rozwiązanie: 4. Ze środka w punkcie O należy wykreślić okrąg jr przechodzący przez pun
więcej podobnych podstron