DSCN0783 (2)

4.2.4. Wzajemne położenie dwóch prostych

Dwie proste w przestrzeni mogą być:

a)    wzajemnie do siebie równoległe,

b)    przecinające się,

c)    wichrowate.

Jeśli dwie proste są do siebie równoległe, to ich jednoimienne rzuty nież równoległe między sobą (rys. £-19).

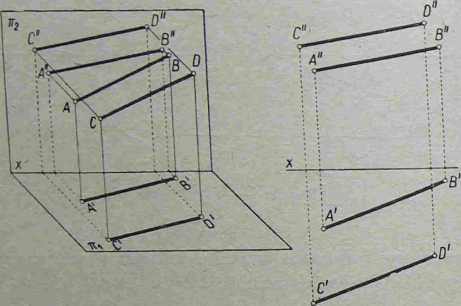
Rys. 4-19. Rzuty prostych wzajemnie równoległych

Jeśli dwie proste przecinają się ze sobą, to ich jednoimienne rzuty również i się ze sobą przecinają, przy czym rzuty punktu przecięcia się tych prostych i

leżą na jednej prostej prostopadłej do ośi x 1 C^a    (rys* 4-20).

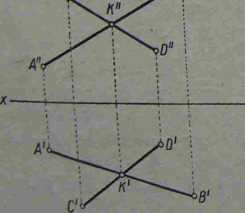
Rys. 4-20. Rzuty przecinających się prostych

Rys. 4-21 przedstawia dwie proste prze* | cinające się pod kątem 90° w punkcie A. V rzucie na rzutnię poziomą n\ otrzymamy ¹ również kąt 90° tylko wtedy, kiedy jedno Tamię będzie równoległe do rzutni poziomej-Uogólniamy to stwierdzenie w następujący sposób: Jeśli rzut dowolnego kąta przedstawia kąt prosty, to odwzorowany kąt wtedy tylko będzie kątem prostym, jeśli przynaj^-mniej jedno jego ramię będzie równoległe do rzutni.

Jeśli dwie proste mijają się w przestrzen' (nie są do siebie równoległe i nie przecinaj? się ze sobą), to takie proste nazywają się prostymi wichrowatymi. Punkty przecięcia jednoimiennych rzutów prostych wichrowatych nie leżą na jednej prostej prostopadłej do osi x (rys. 4-22).

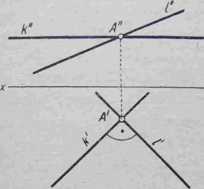
Rys. 4-21. Rzuty prostych przecinających się pod kątem 90°

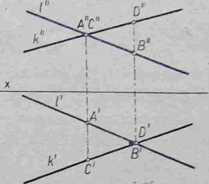
Rys. 4-22. Rzuty prostych wichrowatych

4.2.5. Wyznaczanie rzeczywistej długości odcinka

Wiemy, że rzut danego odcinka jest równy odcinkowi tylko wtedy, kiedy odcinek jest równoległy do płaszczyzny rzutów. Bardzo często jednak położenie odcinka, jako krawędzi przedmiotu rzutowanego, jest ukośne względem wszystkich rzutni. Aby na podstawie rzutów takiego odcinka określić jego rzeczywistą długość, posługujemy się najczęściej dwiema metodami: a) metodą kładu i b) metodą obrotu.

Na rys. 4-23 mamy przedstawiony odcinek AB w rzutach, położony dowolnie w przestrzeni w układzie dwóch rzutni poziomej n_x i pionowej jr₂. podstawie

Rys. 4-23. Wyznaczanie rzeczywistej długości odcinka metodą kładu

jego rzutów mamy określić rzeczywistą długość tego odcinka. Rys. 4-23a w sposób poglądowy ułatwi nam zrozumienie metody, którą nazywamy metodą kładu. Figura ABB'A' jest trapezem, którego boki są następujące: AB — to dany odcinek; BB' — to wysokość jednego punktu B danego odcinka; A'B' — to rzut poziomy odcinka; AA' — to wysokość punktu A danego odcinka. W rysunku rzutowym znane nam są tylko trzy boki tego trapezu, a mianowicie

5* 67