DSCN1166

7.18.    Wskazówka. Przedstawić w postaci iloczynu różnicę sin x — sin y i skorzystać z nierówności

|sinx| < |x|.

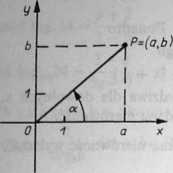
7.19.    Jeżeli a = b = 0, to nierówność jest prawdziwa. Jeżeli a, b nie są jednocześnie zerami, to przyjmując: a = rsina, fe = r cos a, r² = a² + b², otrzymujemy

|«sin.v + A>sin.v| = r|cos(v - ?l! ś r. (rys. 7.19)

7.20. Dla przykładu podajemy rozwiązania punktów a) oraz I)

, ... . tr 2tt 4tt

a) Niech cos-cos—cos— = x. Mnożąc obie strony tej rowno-

, .    „.7t.27t.47t

sci przez 8 sin-sin—sin—, po przekształceniach otrzymujemy

.27t.47l.87t    . 71 . 271 . 47t,

sin y sin y siny = 8x (sin - sin y sin y).

Stąd 1 = 8jc, czyli x = -0 Pomnóżmy daną sumę przez 2sin-.

Otrzymamy wtedy

. 7t 2ti 3ti, „ . 7t (cos- — COSy + y)'2stn- =

= (ŻCOSyCOS- -COSy)-2sin- =

2ll 7t . 71    . 7t 27t

= 4C0SyC0S-Sin- — 2sm- COSy =

. 4n , . 3n . n.

= sin— - (siny - sin-) =

. n ,    . 4n . 3n

= sin-, bo siny == siny.

_    it 2n 3n 1

Zatem cos- — cosy + cosy = -.

a) 5’ ^b) Ł’ ^C) T6’ ^d* ²<^{3 +} V^ ^{e) 35, 0} J’ ^l-

²'²^’ ^S cos a-cos (a + r) cos (a + r)-cos(a + 2r)

_1___

cos[a + (n — l)r] • cos(a + nr)

1 sin(a + r — a) sinr cos a ■ cos(a + r)

1 sin (a + 2r — a — r)

-f- — ¹    *    -    ~~ x ... -f”

sinr cos (a + r) cos (a + 2 r)

1 sin [a + nr — a — (n — 1 )r] sin r cos [a + (n — l)r]cos (a + nr)

= -■— [(tg(a + r) - tga) + (tg(a + 2r) - tg(a + r)) +

+ ... + (tg(a + nr) — tg(a + (n — l)r))] =

⁼ sinr C“ ^tg“ ^{+ tg}*^{a +} "^r^ ⁼

1 sin(a + nr —a) sin r cos (a + nr) cos a 1    sin nr

sinr cos (a + nr) - cosa _    sin (nr)

sin r cos a cos(a + nr)'

7.22. Wskazówka. Najpierw wykazać, że istnieje nieskończenie wiele liczb naturalnych dodatnich spełniających nierówność

sin t > - i oznaczyć ten zbiór przez A. Następnie wykazać, że dla

każdej liczby rzeczywistej 2a istnieje liczba t₀eA taka, że t₀ > 2a i stąd wyprowadzić tezę twierdzenia.

189