DSCF6571

98

pr_L* Hb|g9 |

k¹

opisującym ruch wahadła matematycznego o długości / = — + </; d jest tutaj

odległością osi obrotu od środka ciężkości bryły, k nazywa się ramieniem bezwładności i jest związane z masą bryły i jej momentem bezwładności /„, mierzonym w przypadku, gdy oś obrotu przechodzi przez środek ciężkości, zależnością:

(2)

1₀ = mk¹

Minimalną wartość okresu znaleźć można przyrównując do zera pochodną 1, obliczoną ze względu na d:

^ + d\ = -~ + l=0-*k= ±d    (3a)

a stąd

T

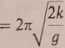
(3b)

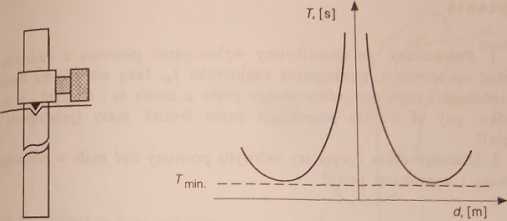
lys, 16. Uchwyt mocujący    Rys. 17. Zależność okresu drgań T od odległości osi

wahadło    obrotu od środka ciężkości wahadła d

Okres drgań znajdujemy dla kilkunastu różnych wartości d, mierząc czas 1 kilku wahnięć* n:

n

3, Opracowanie

Wyznaczenie minimalnego okresu drgań T_min z wykresu (rys. 17) pozwala, po wykorzystaniu związków 2 i 3a, na znalezienie k i g. Ponieważ jednak odczytana z wykresu wartość T_min. obarczona jest dużym błędem, zastosujemy inną metodę, zapisując w nieco zmienionej formie równanie 1:

471^

dT² = —(k² + d²)    (4)

albo y = a + bx, po zastosowaniu podstawienia y = dT², x = d². Współczynniki a i b wynoszą odpowiednio 4n²k²/g i 4n²/g. W tak skonstruowanej skali funkcyjnej wyniki przedstawione na rys. 17 ułożą się w przybliżeniu wzdłuż linii prostej, przecinającej oś x w punkcie x₀ = -k². Parametry x₀ i 'li znaleźć można graficznie lub metodą najmniejszych kwadratów. Ramię bezwładności bryły i przyspieszenie ziemskie znajdujemy wówczas ze związków: M g = 4n²/b.

' Pomiar dokonywany jest elektronicznie - z bardzo wysoką precyzją.

1

Pomiary

Wahadłem użytym w doświadczeniu jest metalowy symetryczny pręt, umieszczony w uchwycie unieruchamianym za pomocą zacisku (rys. 16). Uchwyt powinien być możliwie mały i lekki w porównaniu z prętem.

Pomiary polegają na badaniu okresu drgań wahadła w zależności od odległości osi obrotu od środka ciężkości. Okres staje się „nieskończony” dla d = 0 (rys. 17).