MG!68

1	^V12	^V13	Tl 14	Tl 15	Tl 16		°1
1	n	*33	G44	G55	G«
^V21	1	^V23	Tl24	Tl 25	Tl 26
	i		G»	g3J	n		2
^V31	^V32	1	Tl34	Tl35	Tl 36
	1	1	G«	II	G«	X	^u3
n4i	^42	^43	1	1*45	P 46		°4
		i		G55
nsi	ns?		P54	1	1^56
		gj					°5
n6i	^62	Tl 63	Pfi4	ł*"65	1
£,i	Ę	*33	G44	g		]	°6

(4.19)

Można dowieść, że macierz podatności S» jest macierzą symetryczną, tzn.

11    (4.20)

W związku z tym, macierz podatności w ogólnym przypadku jest opisana przez 21 niezależnych stałych technicznych:

•    trzy moduły Younga

E_ij, i = 1,2,3 (nie sumować);

•    trzy moduły Kirchhoffa

JP

j = 4,5,6 (nie sumować);

trzy współczynniki Poissona; ze względu na symetrię macierzy podatności muszą być spełnione trzy równania

(4.21)

1,2,3 (nie sumować);

dziewięć tzw. współczynników wpływu pierwszego rodzaju, pozwalających opisać wpływ naprężeń normalnych na odkształcenia postaciowe, jak też wpływ naprężeń stycznych na odkształcenia liniowe; ze względu na symetrię macierzy podatności spełnionych musi być sześć równań

l = 1,2,3 k = 4,5,6

(nie sumować);

(4.22)

trzy tzw. współczynniki wpływu drugiego rodzaju |i , pozwalające opisać wpływ naprężeń stycznych działających w jednej płaszczyźnie na odkształcenie postaciowe w innej płaszczyźnie; ze względu na symetrię macierzy podatności muszą być spełnione trzy równania

iii! a , n,m = 4,5,6 (nie sumować).    (4.23)

G/tn ^*mm

W celu opisania stanu odkształcenia dowolnego sprężystego ciała anizotropowego należałoby więc wyznaczyć doświadczalnie aż 21 niezależnych technicznych stałych materiałowych.

W rzeczywistych materiałach konstrukcyjnych sytuacja przedstawia się znacznie korzystniej ze względu na występującą w nich symetrię struktury budowy materiału, rzutującą wprost na postać macierzy podatności, tzn. na rodzaj anizotropii.

Należy zastanowić się w związku z tym nad wpływem budowy materiału na jego właściwości — w tym przypadku na postać macierzy podatności.

Przyjmuje się założenie, że w budowie rozpatrywanego materiału występuje płaszczyzna symetrii struktury (n_#), np. płaszczyzna 1—2 (rys. 4.2).

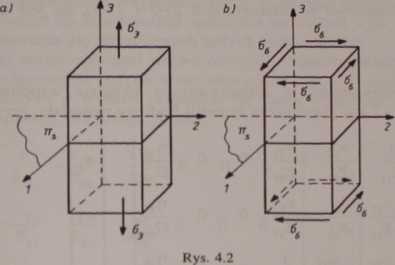
W wyniku przyłożonego stanu naprężenia, spełniającego warunki symetrii, mogą pojawić się jedynie te składowe stanu odkształcenia, które również spełniają warunki symetrii. W związku z tym, na skutek działającego stanu naprężenia (rys. 4.2a)

Oj # 0, O, - Oj “ 0₄ - Oj ■ 0₆ - 0

nie mogą wystąpić składowe stanu odkształcenia e₄ i e_s (odkształcenia postaciowe w płaszczyznach 2—3 i 1—3). Jest to możliwe w układzie współrzędnych zgodnych z rys. 4.2 tylko wtedy, jeżeli zerować się będą współczynniki wpływu

97